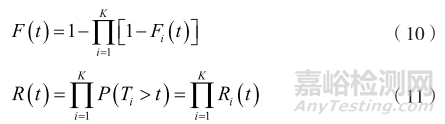本文針對某伺服機構控制器電路板采用故障物理方法進行失效分析,然后在不同溫度應力下開展該電子產品溫升試驗和熱仿真,之后基于Coffin-Manson模型進行產品焊點疲勞壽命仿真并求解各元器件壽命分布,最后構建競爭失效模型進行電路板壽命預計。通過溫度應力試驗得到了關鍵元器件溫升值在23℃~31℃范圍內,基于CRAFE熱仿真得到了產品各元器件溫度,應用Coffin-Manson模型得到了元器件壽命分布,運用競爭失效方法計算了產品失效概率函數,評估了產品工作10年的可靠度為0.94,在可靠度指標為0.9時其工作壽命為12.11年。本文基于溫度應力試驗和熱仿真,通過進行故障物理分析和元器件競爭失效分析有效評估了電子產品工作壽命,對其他類似電子產品可靠性分析提供了一定參考。
引言
隨著軍事科學技術的發展和新時期裝備的迭代更新,現代裝備對可靠性的要求越來越高,研究發現在環境引起的裝備故障中電子產品的失效比例在所有統計試驗中占比最大。電子產品作為裝備關鍵組成部分對保證裝備戰備完好性、任務成功性以及維修保障性等十分重要,同時裝備中電子產品也呈現出研制周期短、新技術大量應用、可靠性指標越來越高的發展趨勢,因此如何有效分析和提升裝備電子產品的可靠性成為亟待解決的問題。
可靠性分析包括基于概率統計和基于故障物理模型兩個方向,然而,在無故障樣本情況下,基于概率統計方法面臨應用上的局限性。美國馬里蘭大學最先提出并展開了基于故障物理(Physics of Failure,PoF)模型的可靠性分析技術研究,之后廣泛應用于美國的航空航天和陸軍的裝備研究。基于故障物理的試驗通常需要耗費大量資源,而仿真具有成本低、可重復等優勢,現今多數研究采用試驗仿真相結合的方式探索電子產品故障機理模型。
國內外學者在電子產品故障物理分析、疲勞模型研究、可靠性仿真、壽命預計等方面已取得許多成果。Jiao J等給出了電子產品故障原因統計結果,其中溫度占比43.3%,這溫度和振動應力已成為電子產品可靠性研究的重點。Wilman A等針對電子產品進行了基于故障物理分析的壽命預測研究,但其對可靠性求解過程分析不充分。胡博等針對機載電子產品進行了可靠性仿真試驗的應用探索。欒家輝等針對電子產品薄弱環節進行了單應力和多應力累積損傷仿真分析并給出產品壽命預測結果。陳穎等分析了電子產品部分元器件失效模式、機理與故障物理模型,研究了一種基于故障物理的產品可靠性仿真方法,但對有熱源產品的溫升參數研究存在不足。黃姣英對故障物理分析中常用焊點疲勞模型進行了綜述。李寶蘭針對舵機控制電路板進行了熱分析及基于Coffin-Manson模型的焊點疲勞壽命預測研究,該研究只針對電路板部分焊點進行了分析。現今,對于電子產品可靠性分析雖已有大量研究,但針對裝備典型電子產品基于故障物理的可靠性分析應用研究仍不充分,現有研究多針對電子產品薄弱環節進行分析,仍需將產品多個關鍵元器件納入整體壽命評估研究中。
本文針對某伺服機構控制器電路板,運用故障模式、機理及影響分析(FMMEA)方法進行產品故障物理分析并確定基于溫度應力的故障物理模型;之后分析確定產品組成和材料參數,通過溫度應力試驗和熱仿真相結合的方式分析電路板溫度分布;進一步,通過焊點疲勞模型計算疲勞壽命,求解元器件疲勞壽命分布;最后結合競爭失效分析實現電子產品可靠工作壽命有效評估。
失效物理模型分析
1、電路板結構
本文研究實例對象為某裝備伺服機構控制器電路板,該產品屬于典型電子產品。電路板整體較小,長126mm、寬54mm、厚2mm,其中部分元器件質量和體積相對較大。該電路板硬件主要由DSP及外圍電路模塊、功率驅動模塊、模數轉換模塊和接口模塊等組成,PCB焊接各類電阻、電容、集成電路、電連接器等元器件。
圖1 電路板實物圖
2、失效物理分析
使用FMMEA方法對電路板進行潛在的故障模式和機理分析。電路板工作環境條件良好,可排除振動、斷裂、靜電和輻射等故障因素,同時電路板元器件滿足軍用標準,自身故障發生可能性遠小于焊點發生故障可能性。實際使用時,溫度變化會導致電連接部位焊點熱疲勞失效,因此本文主要進行基于焊點熱疲勞的電路板失效分析研究,該產品部分元器件故障物理信息如表1所示。
表1 部分元器件的FMMEA
3、Coffin-manson模型
焊點疲勞壽命預測模型主要基于塑性變形、蠕變變形、斷裂參數、能量等進行構建,研究表明材料的塑性應變逐漸累積將會引起疲勞失效,對于電路板故障物理失效分析常用焊點熱疲勞模型為基于應變的Coffin-Manson模型,該模型體現了應力與循環周期的關系,模型公式如下:
式中:
 —器件失效所經歷的循環周期;
—器件失效所經歷的循環周期;
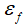 —疲勞系數,該系數與材料相關,對于63Sn37Pb,該值取 0.325;
—疲勞系數,該系數與材料相關,對于63Sn37Pb,該值取 0.325;
c—疲勞指數,該指數與材料相關;
 —剪切應變范圍。
—剪切應變范圍。
式中:
—焊點溫度循環中平均溫度;
—最高溫恒定時間;
f —溫度循環頻率。
式中:
F —應力范圍因子,
L—元器件長度,
h—焊點高度,
 —元器件殼體熱膨脹系數,
—元器件殼體熱膨脹系數,
 —基板熱膨脹系數,
—基板熱膨脹系數,
 —器件外殼工作溫度,
—器件外殼工作溫度,
 —基板工作溫度,
—基板工作溫度,
 —初始溫度。
—初始溫度。
常見焊點橫截面如圖2所示。
圖2 焊點橫截面示意圖
已知溫度循環載荷作用下元器件與PCB基板均受溫度影響發生脹縮,PCB板焊接多種材料的元器件,不同元器件相對基板產生應變,進而導致焊點疲勞損傷。
溫度試驗與仿真
通過分析電路板組成,研究文獻確定各部分的材料類型、熱膨脹系數、彈性模量、導熱系數等材料參數,對于本文研究的電路板,采用溫度試驗和熱仿真相結合的方式確定各元器件溫升參數,用于計算焊點疲勞壽命。
一.溫度應力試驗
1.溫升試驗環境搭建
通過梳理元器件清單并根據實際使用情況,得到該電路板4個發熱功率較高且容易產生焊點熱疲勞的關鍵元器件。對于1號、2號和3號器件分別使用編號為S01、S02、S03的熱電偶分別采集電源模塊溫升數據,由于4號集成電路尺寸較大,使用S04和S05號2個熱電偶在不同位置采集溫度數據,之后按照控制器實際安裝方式進行組裝,進一步通過連接供電電源、數采設備、計算機,并將該控制器放入溫箱組成試驗系統,熱電偶貼片和測試系統如圖3所示。
圖3 溫度應力試驗環境搭建
2.溫升試驗流程
將溫箱分別調整到25℃、35℃和45℃進行試驗并采集數據,設定每種溫度應力下數據采集時長為35分鐘、采樣頻率10Hz。試驗環境搭建完成后,首先將溫箱溫度設置為25℃,待溫箱溫度穩定至25℃后觀察計算機顯示的熱電偶感知溫度,數值穩定至25℃時打開電路板電源使其正常工作,通過計算機記錄設備采集的溫升數據,完成該溫度應力下試驗后關閉電路板電源。
3.溫升試驗結果分析
試驗得到25℃、35℃和45℃溫度應力下電路板關鍵產熱元器件溫升數據,通過中值濾波和均值濾波方法對信號數據進行處理,各測點在3種溫度環境下的溫升曲線如圖4所示。
圖4 熱電偶測量溫升曲線
電路板在不同溫度環境應力下運行時同一位置溫升速度隨溫度升高逐漸變慢最后趨于穩定;電路板不同位置工作運行溫升量和熱平衡值存在差異,例如1號位置(S01)在不同溫度應力下熱平衡溫升值均比2號位置(S02)低5.5℃左右,比3號位置(S03)低4.3℃左右。根據熱電偶采集數據,計算得到在25℃,35℃和45℃環境溫度下各熱電偶測量點熱平衡時的溫升數據,熱平衡溫升隨溫度變化的溫升曲線如圖5所示。
圖5 各監測點溫升規律圖
從圖5中可知熱平衡時各測點溫升在23℃到31℃內,隨著環境溫度的升高穩態溫升量略有下降趨勢,同一位置不同溫度應力下溫升差均小于1℃。將試驗溫升結果作為可靠性仿真模型的參數輸入,用于進行電路板溫度分布仿真分析。
二. CRAFE熱仿真
1.仿真模型構建
本文基于CRAFE軟件進行電路板的溫度應力仿真分析,該軟件可提取各元器件仿真過程溫度參數值。使用AD(Altium Designer)軟件將設計的電路板模型轉換為ODB++模型導入CRAFE軟件并生成相應的幾何模型。該模型主要包括元器件層、絲印層、鉆孔層、阻焊層、銅層、機械層等,模型如圖6所示。
圖6 電路板模型圖
2.邊界條件設定
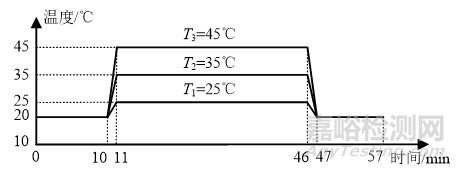
熱仿真過程設置電路板為自由狀態,根據溫度應力試驗設置對應仿真試驗剖面和器件溫升參數,對于不同溫度應力采用相同的環境溫度變化趨勢,構建3種溫度應力下的環境剖面如圖7所示。
圖7 仿真試驗剖面
選取4個關鍵發熱元器件作為溫升參數設置點,將溫度試驗結果輸入仿真模型。在溫度試驗過程中對于4號位置通過熱電偶獲取了兩組溫升數據,因此模型4號位置對應元器件溫升參數設置為S04和S05熱電偶得到溫升的均值。
圖8 溫升參數設置點
3.電路板熱仿真
使用仿真軟件在25℃溫度應力仿真試驗剖面下進行電路板熱仿真,得到三維溫度云圖結果如圖9所示,基于溫度云圖提取產品各元器件溫度。
圖9 電路板熱仿真結果(25℃)
在25℃、35℃和45℃三種溫度應力下通過仿真可以得到產品溫度應力云圖和所有位置的溫度數據,根據以下公式計算溫升設置點仿真與試驗結果的相對誤差,仿真與試驗對比結果如表2所示。
式中:
s —仿真溫度結果;
e —試驗溫度結果;
p —相對誤差。
表2 仿真與試驗結果對比
仿真結果和試驗結果相對誤差均小于5%。因此通過仿真得到的產品各位置溫度具有較強可信度,同時表明在CRAFE軟件中設置的各參數較為準確,可用于電路板各元器件溫度仿真提取。
產品壽命預計
1、 Coffin-Manson壽命預計
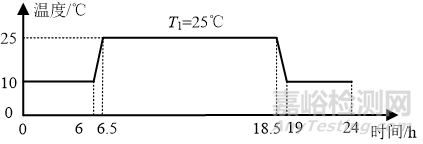
將改進后的 Coffin-Manson 熱疲勞模型作為壽命預計的故障物理模型,設置電路板全壽命周期經歷的溫度循環任務剖面如圖10所示。
圖10 任務剖面
根據各元器件封裝、引腳、焊點和溫度等方面參數輸入,將任務剖面作為仿真條件輸入,通過每周一次的溫度循環仿真對產品各個元器件進行基于焊點熱疲勞故障的壽命預計。得到各元器件預計失效時間(Time to Failure,TTF),部分結果如表3所示。
表3 部分元器件壽命預計結果
2、Weibull壽命分布分析
在溫度循環載荷條件下,元器件的焊點疲勞壽命的隨機性通常可采用 Weibull 分布或對數正態分布進行描述。本文使用雙參數威布爾分布表征元器件壽命分布特性,基于壽命預測結果仿真得到元器件失效概率分布,元器件累積失效概率和概率密度函數表達式如下:
式中:
m—形狀參數;
η—尺度參數。
已知雙參數威布爾分布 MTTF 可表示為:
設置經驗參數m=3并根據各元器件焊點疲勞失效時間計算得到元器件壽命分布參數 ,部分元器件壽命分布參數計算結果如表4所示。
,部分元器件壽命分布參數計算結果如表4所示。
表4 元器件壽命分布參數結果
3、競爭失效分析
將電路板元器件視為串聯可靠性分析系統進行評估,根據各元器件失效概率分布,應用競爭失效理論計算電路板總體壽命分布。在電路板使用過程中,最早失效的元器件將導致電路板失效,假設每個元器件的失效時間為Ti,則電路板的失效時間為:
其中:K為電路板元器件個數。設Fi(t)是元器件 i 的累積失效概率分布,電路板的累積失效概率分布函數和可靠度函數分別為:
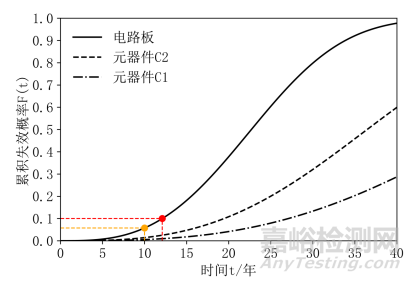
通過競爭失效公式求解得到電路板服從的威布爾失效分布的參數結果為m=3、η=25.66。電路板累積失效概率分布結果如圖11所示。
圖11 電路板壽命分布預計結果
由計算結果可知,運用競爭失效分析得到電路板的可靠度小于各元器件可靠度。電路板在規定任務剖面下使用10年的預計累積失效概率為5.75%,可靠度約為0.94。在產品實際可靠性設計中,若以0.90為可靠度指標計算剩余使用壽命,則可設定產品累計失效概率F(t)=0.1,通過威布爾分布逆函數計算得到產品預計出現故障的時間為12.11年。
結語
文中針對裝備典型電子產品提出了一種基于溫度應力試驗的可靠性分析方法,用于評估了某伺服機構控制器電路板壽命。通過開展溫度應力試驗和熱仿真,獲得關鍵元件器溫升特性和溫升參數,通過應用Coffin-Manson模型得到了元器件壽命分布,結合元器件競爭失效分析進行了電路板工作壽命預計。論文主要針對故障物理中溫度環境變化導致焊點熱疲勞對電子產品可靠性的影響進行了研究,在后續工作中還需綜合考慮其他復雜環境因素和失效模式,進而使得可靠性分析更加全面和準確。
引用本文:曹敬帥,秦強,張生鵬,楊培,喬洪凱.基于溫度應力試驗的電子產品可靠性仿真分析[J].環境技術,2023,41(03):31-37+43.




 —器件失效所經歷的循環周期;
—器件失效所經歷的循環周期;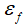 —疲勞系數,該系數與材料相關,對于63Sn37Pb,該值取 0.325;
—疲勞系數,該系數與材料相關,對于63Sn37Pb,該值取 0.325; —剪切應變范圍。
—剪切應變范圍。
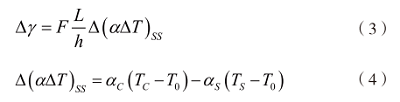
 —元器件殼體熱膨脹系數,
—元器件殼體熱膨脹系數, —基板熱膨脹系數,
—基板熱膨脹系數, —器件外殼工作溫度,
—器件外殼工作溫度, —基板工作溫度,
—基板工作溫度, —初始溫度。
—初始溫度。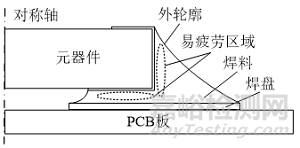











 ,部分元器件壽命分布參數計算結果如表4所示。
,部分元器件壽命分布參數計算結果如表4所示。