PET是應用最廣泛的芳香族聚酯之一。生活中常見的礦泉水、可樂、果汁等包裝瓶的材料大多是PET材料制作的。PET具有很多優良的特性,例如:機械強度高、透明性好、化學性穩定等。由于PET具有如此多的優良的特性,自二十世紀八十年代問世以來便迅猛發展,逐漸成為人們生活中不可缺少的材料。
PET必須具有非常好的耐熱和耐熱氧老化性能。而PET中含有大量相對活性較高的酯基,在熱氧的作用下容易發生分子鏈斷裂的熱降解反應。熱降解會影響PET的性能,同時PET的降解產物中含有諸如乙醛這種對人體有害的物質。所以,研究PET的熱降解反應和推測其使用壽命具有非常重要的實際意義。
通過熱分析技術,分別以5K/min、10K/min、15K/min、20K/min的升溫速率測得相應的熱分解曲線。由熱分解曲線通過Kissinger法和Freeman-Carroll法求得PET的活化能E、指前因子A和反應級數n。同時通過TG恒溫法測得PET在360℃、370℃、380℃、390℃、400℃下失重10%經歷的時間,將此時間當作PET的壽命,通過阿侖尼烏斯方程進行線性擬合最終得到PET熱分解壽命方程。
1、實驗
1.1實驗材料和儀器
聚對苯二甲酸乙二醇酯(PET),礦泉水瓶專用粒料。
1.2實驗方法
TGA熱分解實驗:先打開恒溫水浴和保護氣(氮氣,20mol/min),將實驗氣氛設為空氣(流速:50mol/min),經過一段時間穩定后打開TGA,用鑷子將氧化鋁坩堝放置在TGA天平上,然后去皮取下,從PET粒料上切下重5mg~10mg的試樣,用鑷子將試樣放到氧化鋁坩堝中,最后將氧化鋁坩堝再次放到TGA天平上,升溫速率依次設為5K/min、10K/min、15K/min、20K/min。
TGA恒溫實驗:設置實驗氣氛為空氣(流速:50mol/min),保護氣氛為氮氣(20mol/min),分別設定實驗溫度為360℃、370℃、380℃、390℃、400℃,機器將以能達到的最大升溫速率快速上升到設定溫度。
2、數據處理
2.1Kissinger法
(1)式中:Tp是DTG曲線中微峰溫度(K),β是升溫速率(K/min),E是表觀活化能(J·mol-1),R是氣體常數(約為8.314,單位J·mol-1·K-1),A是指前因子(min-1)。
分析5K/min、10K/min、15K/min、20K/min下PET的TG-DTG曲線,得到不同升溫速率β下所對應的DTG曲線的Tp(峰值溫度),用ln(β/Tp2)對
1/Tp作圖,通過線性擬合可以求出活化能E和指前因子A。
2.2Freeman-Carroll法
(2)式中:為分解率,T為熱力學溫度(K),A為指前因子(min-1),β是升溫速率(K/min),E為活化能(J·mol-1),R是氣體常數(約為8.314,單位
J·mol-1·K-1)。
假設適當的反應級數,以ln[(d/dT)/(1-)n]對1/T作圖,由直線的斜率求E,由直線的截距求A。
3、結果與討論
3.1PET熱分解曲線
圖1PET的失重(TG)曲線
Fig.1TheweightlosscurvesofPET
由PET的TG曲線可以看到PET的在空氣中的熱分解分為兩個階段:第一個階段的起始點溫度約在300℃左右,這個階段是PET的主要失重階段,PET大分子鏈在此階段大量分解,第二階段的起始溫度約在450℃左右,在整個PET分解過程中所占的比重不大,這部分分解主要是PET中有未反應完的單體和小分子物質。當第一階段失重發生時,
PET已經開始老化失效,由于本實驗的主要目的是推測PET的使用壽命,所以只考慮PET分解的第一個階段。由圖1、圖2同時可以看到:隨著升溫速率的升高,PET的TG曲線和DTG曲線都有向高溫方向移動的傾向。
圖2PET的DTG曲線
Fig.2DTGcurvesofPET
3.2Kissinger法求動力學參數
由PET在5K/min、10K/min、15K/min、20K/min下的TG曲線和DTG曲線可以得到表1數據。
表1PET熱分解實驗數據
Table1ExperimentaldataofthermaldecompositionofPET
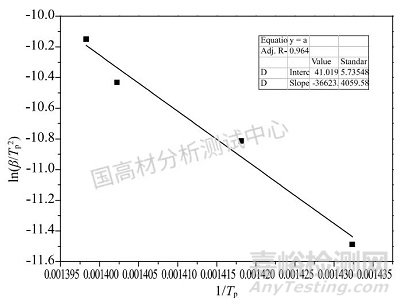
由表1數據,用ln(β/Tp2)對1/Tp作圖,通過線性擬合得到圖3。
由圖3的線性擬合曲線可得到擬合方程:
y=-36623x+41.02
通過計算可以得到表觀活化能E約304.48kJ·mol-1,指前因子A約為2.4×1022min-1 。
圖3Kissinger法線性擬合圖Fig.3Kissingermethodoflinearfitting
3.3Freeman-Carroll法推斷熱分解機理
用5K/min升溫速率的TG-DTG曲線來推斷PET熱分解機理。PET的TG-DTG曲線如圖4所示。
圖4升溫速率5K/min時PET的TG-DTG曲線
Fig.4TG-DTGcurvesofPETatβ=5K/min
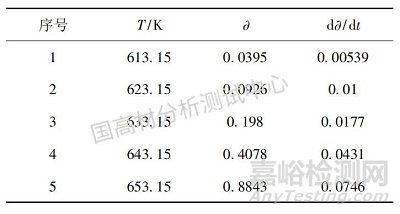
由圖4可得表2數據。
表2升溫速率5K/min時PET的失重數據
Table2WeightlossdataofPETatβ=5K/min
將表2的數據用Freeman-Carroll法處理,假設n的值為0.5、1、1.5、2。通過處理后的數據和假設的反應級數n,可以計算得到不同反應級數下的表觀活化能E和指前因子A,當計算得到的表觀活化能E值和指前因子A值與Kissinger法求得的活化能E和指前因子A大致相同時,此時相對應的n為該反應最可能的反應機理函數,此時求出的表觀活化能E和指前因子A即是該反應的表觀活化能和指前因子。計算結果見表3。
表3Freeman-Carroll法求反應動力學參數
Table3Carroll-Freemanmethodtoobtain thekineticparameters
由表3數據可知,當n=0.5時,Freeman-Carroll法求得的活化能E和指前因子A與Kissinger法求得的結果較為接近,且此時線性相關較好,故此時的機理函數為最可能的反應機理函數。將兩種方法結果取均值得:E=302.36kJ·mol-1,A=4.2×1023min-1。
3.4阿侖尼烏斯方程推測PET的熱分解壽命方程
通常認為,溫度的升高會使化學反應速率相應提高。這兩者之間的關系通常使用阿侖尼烏斯公式來描述:
KA·e-E/RT(1)
式(1)中,K是反應速率常數(min-1),A是指數因數(min-1),T為熱力學溫度(K),R是摩爾氣體常數[8.314J/(mol·K)],E是活化能(J/mol)。化學反應關系以式(2)表示:
Fx(t)=K(t)·t(2)
式(2)中,F(x)是反應關系的函數,t是反應時間。
將式(2)變換:
lnti=E/RTi+B(3)
在實驗選取的溫度內,活化能E為常數,將實驗數據作lnti與1/Ti的線性擬合方程即可得到老化壽命方程。
將PET在TGA中分別在360℃、370℃、380℃、390℃、400℃下恒溫,且以失重10%作為壽命終點。得到數據見表4。
表4TG恒溫失重10%經歷的時間
Table4ThetimeofTGconstanttemperatureweightlessness10%
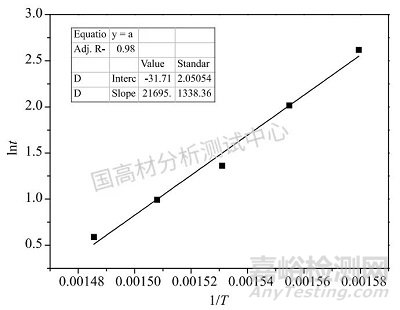
用公式(2)對表4數據進行線性擬合得到圖5。
圖5PET失重10%的線性擬合曲線
Fig.5LinearfittingofPETofweightlessness5%
由擬合曲線得到PET熱分解壽命方程:lnt=21695/T-31.71
4、結論
本實驗通過熱分析技術在不同的升溫速率下測得PET的表觀活化能E約為302.36kJ·mol-1,指前因子A約為4.2×1023min-1,反應級數n為0.5。通過TG恒溫技術分別測得360℃、370℃、380℃、390℃、400℃下失重10%所用的時間,并且通過阿侖尼烏斯方程進行線性擬合得到PET熱分解壽命方程:lnt=21695/T-31.71。此結果對研究PET的加工、降解、壽命評估有一定的指導意義。