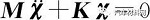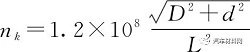摘要:為研究萬向節傳動軸的動態特性,采用了有限元分析法對萬向節傳動軸進行約束模態分析,包括固有頻率和振型,并結合試驗驗證結果,確定了最適用傳動軸臨界轉速的接觸算法,保證了有限元法的有效性;進一步研究了傳動軸臨界轉速的影響因素。結果表明:傳動軸長度對臨界轉速影響較大,并呈現二次非線性關系,而材質對臨界轉速影響較小;萬向節作為傳動軸上的關鍵部件,過大的動載荷會縮短其使用壽命,進而造成整根傳動軸失效,而其動載荷的大小可由兩端所受反力間接表征。通過計算傳動軸固定端和花鍵副處的支反力,為萬向節動載荷受力情況提供判斷依據,進而指導萬向節最優壽命的傳動軸總成設計。
引言
汽車行駛時傳動軸高速旋轉,受到周期性的不平衡質量產生的離心力以及發動機往復慣性力的沖擊,當附加激振力的頻率與傳動軸的固有頻率接近時,將引發傳動系統的共振,表現為劇烈抖動。傳動軸共振時的轉速即為臨界轉速,本文結合傳動軸材料與結構對其臨界轉速及萬向節受力進行分析,為設計提供理論依據。
目前,傳動軸臨界轉速的計算一般采用經驗公式法和有限元分析法。其中經驗公式法具有計算簡單迅速的優點,因此在傳動軸傳統設計中被廣泛應用。但經驗公式法僅對等截面傳動軸的臨界轉速計算效果較好,而對于滑動型傳動軸總成,花鍵軸處截面積較軸管處更小,按經驗公式計算誤差大,具有較大局限性,且需要進行大量重復的傳動軸成品模態試驗,無法為前期開發提供較精確的指導。有限元模態分析非常適用于復雜形狀傳動軸的計算,在現有研究中應用廣泛。尹榮棟等[1-2]采用有限元模態分析校核某傳動軸是否會在行駛中產生共振。尹長城等[3]同樣采用有限元方法分別計算了分段傳動軸的單段自由模態和總成約束模態,提出多段傳動軸的振動較大處為中間連接部分。王繼紅等[4]在子系統基礎上,引入帶底盤傳動軸模型進行模態分析,拓展了造成整車振動和噪聲的因素。除此之外,管徑[4]、中間支撐剛度[5]對固有頻率的影響也在不同文獻中被探討。然而,在以上研究中,幾何模型處理、連接關系、接觸關系的設置各有差異。本文提出一種有限元模態分析方法并通過試驗結果證明其有效性,進一步分析傳動軸動態特性,同時作為傳動軸的關鍵結構,萬向節在傳動軸總成不同臨界轉速下的動態特性也是本文研究的重點之一。
1、傳動軸臨界轉速分析
1.1 模態分析理論
模態分析是計算結構振動特性的數值技術,結構振動包括固有頻率和振型,模態分析就是最基本的動力學分析。要研究萬向節傳動軸的動態特性,首先要建立該系統的運動微分方程[6]。一般地,動力學方程為:
(1)
式中:M為質量矩陣;C為阻尼矩陣;K為剛度矩陣;f(t)為力矢量;χ為位移矢量;
 為速度矢量;
為速度矢量;
 為加速度矢量。
為加速度矢量。
由于結構的剛度特性和質量分布影響結構的固有頻率和主振型。系統的無阻尼自由振動方程為:
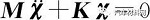
(2)
其對應的特征方程為:
(K-ω2M)φ=0
(3)
式中:ω為系統的固有頻率;φ為模態振型向量。
通過求解式(3)就能得到萬向節傳動軸的固有頻率和振型。
1.2 傳動軸臨界轉速經驗公式法
傳動軸臨界轉速的經驗公式為:
(4)
式中:D為軸管的外徑,mm;d為軸管的內徑, mm;L為傳動軸長度,取兩萬向節中心距, mm。
由經驗公式可知,傳動軸臨界轉速僅與軸管外徑、軸管內徑和兩萬向節中心距有關,與傳動軸總成材質、質量等因素無關。實際上,兩萬向節之間的并非只有形狀規則的軸管,花鍵軸叉因結構不規則,用經驗公式計算勢必會有一定誤差,且不同尺寸的傳動軸配置,花鍵軸叉對臨界轉速的計算結果影響不同。
1.3 傳動軸臨界轉速有限元分析法
在三維建模軟件UG中建立傳動軸總成模型,包括兩端法蘭叉、萬向節總成、花鍵軸叉、防塵罩、花鍵軸、軸管、焊接叉,如圖 1所示。之后導入ANSYS中進行前處理。
圖1 傳動軸總成幾何模型
幾何處理階段去除對模態分析基本無影響的防塵罩、萬向節總成,并將軸管與花鍵軸、焊接叉合并。各部件采用10 mm網格劃分,傳動軸各部位連接和接觸行為見表1。
表1 傳動軸各部位連接和接觸行為
最后,在兩端法蘭叉的螺栓孔處施加固定支撐約束,求解前6階模態,其中1階模態為主要研究目標。傳動軸臨界轉速可由其1階模態對應的固有頻率換算得到:
nc=fc×60
(5)
式中:fc為1階模態對應的頻率,Hz;nc為臨界轉速,r/min。
對于具體的接觸行為,ANSYS通過不同的接觸算法來阻止模型的滲透。常用的接觸算法有以下幾種:懲罰函數法(Pure Penalty)、拉格朗日法(Normal Lagrange)、增廣拉格朗日法(Augment Lagrange)和多點約束法(MPC)。不同算法在算法原理、收斂性和計算精度方面存在一定差異。通過比較不同接觸算法的誤差,選擇更適用于所研究問題的計算方案。
1.4 試驗驗證
在通過有限元方法進行傳動軸模態分析的同時,對傳動軸總成采用整車狀態下的模態試驗,以驗證有限元結果的準確性。傳動軸總成通常采用基于脈沖技術的瞬態激勵測試方法[7-9],即“錘擊法”,將數據采集器以及加速度傳感器組成的臨界轉速測試系統布置在傳動軸軸管上進行敲擊測試。按照以上試驗方案和裝置(圖2),試驗測得臨界轉速平均值為5 690 r/min。
圖2 模態試驗布置
不同接觸算法的計算結果見表2。由表可見,采用MPC接觸算法得到的結果與試驗平均值誤差最小,為6.0%,最適合用于此結構傳動軸總成的臨界轉速計算。這是因為Normal Lagrange和Augment Lagrange較適用于大變形問題中的無摩擦或摩擦接觸;Pure Penalty對接觸剛度比較敏感,適用于允許具有一定穿透的接觸行為;而MPC是點與點之間直接的連接接觸,為線性傳遞關系,因此更適用于綁定接觸和不分離約束。除頻率外,振型也是判斷傳動軸共振狀態的重要信息。傳動軸前6階模態振型如圖3所示,由振型圖可知,傳動軸低階共振表現為劇烈的上下彎曲振動。
表2 不同接觸算法的計算結果

圖3 傳動軸前6階模態振型
2、傳動軸臨界轉速影響因素分析
影響傳動軸臨界轉速的因素有多種,如軸管厚度、傳動軸長度、中間支撐剛度(多節傳動軸)、萬向節及花鍵配合間隙等。本文針對現有模型討論傳動軸長度,即兩端萬向節中心距對臨界轉速的影響。
2.1 長度對臨界轉速的影響
保持其他條件不變,改變傳動軸長度分別取1.58、1.63、1.64、1.66 m,計算得到傳動軸1階固有頻率見表3。
表3 不同長度傳動軸1階固有頻率
根據分析結果繪制傳動軸長度與1階固有頻率關系曲線,如圖4所示。
圖4 傳動軸長度與其1階固有頻率關系曲線
由圖4可知,傳動軸的第1階固有頻率值隨其長度的變化分布近似于一條二次曲線,利用數值分析方法對其4個離散點進行曲線擬合,設頻率與傳動軸長度的關系可用二次方程來表示,則求出的曲線方程為:
fc=786.66L2-2 627.6L+2 296
(6)
傳動軸長度對臨界轉速影響較大,傳動軸1階固有頻率隨著長度減少增大較快。一般而言,傳動軸在運行一段時間后,因磨損、變形等因素會引起自身不平衡量加劇,需要傳動軸的工作轉速不高于臨界轉速的75%[10]。
2.2 材質對臨界轉速的影響
長度為1.66 m的傳動軸保持其他條件不變,將除萬向節以外的其他部件材料換成6061-T6鋁合金,計算得到傳動軸1階固有頻率見表 4。
表4 不同材質傳動軸1階固有頻率 單位:Hz
由表4可知,在傳動軸結構不變的情況下,僅改變材料,即使是更輕的材料,對臨界轉速也基本無影響。
3、臨界轉速下萬向節受力分析
共振狀態下,萬向節受強烈動載荷,過大的動載荷會嚴重影響萬向節壽命,進而造成總成失效,因此有必要對此時萬向節的受力狀態做進一步分析。在后處理結果查看法蘭叉螺栓孔和花鍵副兩處位置的支點力的向量可間接反映萬向節的動載荷受力情況,詳細見表5。
表5 傳動軸特定部位受力情況
由表5可知,不同傳動軸長度下兩端固定處和花鍵副處的受力呈現出明顯差異,長度越長,反力越小,萬向節受到的動載荷也越小,有利于保證其使用壽命。另外,傳動軸材質的改變也會顯著影響萬向節所受動載荷,傳動軸總成更輕的材質可有效降低高速振動工況下萬向節軸承受到的激勵載荷,有利于提高萬向節的使用壽命。
4、結論
(1)通過有限元方法計算了萬向節傳動軸總成的前六階模態,確定其臨界轉速,并與試驗結果做對比,發現接觸算法中MPC算法最適用于帶花鍵型萬向節傳動軸總成的臨界轉速計算,誤差僅為6.0%,保證了有限元法的正確性。
(2)系統性地分析了萬向節傳動軸長度、材質對臨界轉速的影響,其中傳動軸長度對臨界轉速影響較大,呈現二次非線性關系,而材質的影響則較小。
(3)證明了萬向節傳動軸總成質量和長度對萬向節受力影響較大,其中以質量影響最為明顯,因此萬向節傳動軸總成進行輕量化設計可有效降低萬向節受到的外界激振力,從而延長萬向節的使用壽命。
參考文獻:
[1] 尹榮棟,趙振東,陳鴻鍵,等.基于OptiStruct的某型汽車傳動軸模態分析[J].農業裝備與車輛工程,2018,56(7):6-10.
[2] 鄢強,鄧祥豐,吳明春,等.基于ANSYS Workbench的傳動軸靜動態特性分析[J].汽車工程師,2019(6):37-40.
[3] 尹長城,馬迅,陳哲.基于ANSYS Workbench傳動軸的模態分析[J].湖北汽車工業學院學報,2013,27(1):15-17.
[4] 王繼紅,汪凱.汽車傳動軸振動的仿真計算及優化[J].噪聲與振動控制,2014,34(1):109-112.
[5] 陳靜,陳曉梅,魏德永.重型汽車傳動軸模態分析與中間支撐剛度設計研究[J].汽車技術,2014(1):7-10.
[6] 雷玉蓮.基于虛擬樣機技術的汽車傳動軸振動研究[D].重慶:重慶大學,2013.
[7] 尹浚,張丙軍,張涌.錘擊法測汽車傳動軸臨界轉速[J].輕型汽車技術,1998(5):13-16.
[8] 喻鎮濤,熊燕.傳動軸臨界轉速測試方法探討[J].汽車科技,2009(6):72-73.
[9] 孫澤玉,高洪平,余許多,等.連接件對碳纖維復合材料汽車傳動軸振動性能的影響[J].復合材料科學與工程,2020(3):80-83.
[10] 田國富,趙慶斌.基于ANSYS Workbench的汽車傳動軸的有限元分析[J].現代制造技術與裝備,2017(9):42-43.


 為速度矢量;
為速度矢量; 為加速度矢量。
為加速度矢量。