摘要
本文通過解讀分離度Rs與塔板數N,保留因子K,選擇性α之間的關系,為廣大讀者在方法分離過程中采取的改進策略提供理論依據,便于后期方法優化的開展。
色譜理論中,分離度Rs公式有多種表達形式,然而筆者認為,包含塔板數N,保留因子K,選擇性α的表達式最具實踐指導意義。
圖1分離度Rs表達公式
如圖1所示,此公式清晰體現了分離度Rs與塔板數N,保留因子K及選擇性α之間的數學關系。如何利用此公式指導具體的方開發,達到理想的分離效果呢?筆者對此進行簡單解讀。
塔板數N的應用
圖2:分離度Rs與塔板數N之間的關系
分離度Rs與塔板數N之間的關系如圖2所示。由圖可知,分離度Rs與塔板數N在一定區域內近似接近線性關系,隨著塔板數N的增加,分離度Rs會一直增加。正是源于此關系,所以尋找高效的色譜柱成為廣大色譜工作者改善分離的常用手段。
如何挑選高效的色譜柱,我們首先要了解如何估算色譜柱的柱效。
色譜柱柱效估算公式如下所示:
N≈500L/dp
L—色譜柱長度(mm),dp—顆粒直徑(um)
由上述公式可知,柱效N與柱長L成正比,與粒徑dp成反比。因此,只要我們在原來色譜柱基礎上增加柱長、減小粒徑或者同時采取這兩方面的措施,均能做到增加柱效。至于增加的比例,則由上述公式可計算。另外,上述公式簡化為L/dp后則可用于以比較兩根色譜柱是否等效。例如兩款色譜柱,分別為4.6*150mm,3um和4.6*250mm,5um,由公式L/dp可推知,兩者L/dp=50,因此兩款色譜柱可視為等效。目前市面上除了常規全多孔外顆粒色譜柱外,核殼顆粒色譜柱也越來越受到重視,其中一方面就是其出色的柱效。與傳統全多孔顆粒色譜柱比較,其柱效往往提高20%以上。
根據圖1分所揭示的數學關系,我們可利用此公式預判改變柱效N后獲得的分離度Rs。例如,某物質在4.6*250mm,5um的色譜柱上的分離度為1.0,嘗試更換為同款4.6*250mm,3um的色譜柱。由公式推算可知,更換后其達到的分離度約為1.3。因此,利用此公式通過對分離度的預判,可避免不必要的試驗。
保留因子K的應用
圖3分離度Rs與保留因子K之間的關系
分離度Rs與保留因子K之間的關系如圖3所示。在討論分離度Rs與保留因子K之間的關系前,筆者先介紹一下保留因子K的計算公式,如下所示:
K=(tR-t0)/ t0,
t0—死時間,tR—溶質保留時間
由圖3可知,當保留因子K≤5時,通過改變K值,分離度都能得到極大的改善。當保留因子K≥10,通過改變K值,分離度得到的改善卻極小。因此,方法開發過程中,如果色譜峰的保留因子K≤5,此時通過改變K值便能有效的改善分離。如果色譜峰的保留因子K≥10,此時通過改變保留因子K將會收效甚微。因此當保留因子K≥10時,改變其他參數將會更加有效。
如圖4案例所示,當K=10時,二者的分離度為2.07;當K=20時,二者的分離度僅為2.16。雖然二者分離度略有增加,但此時付出的代價卻是檢測時間的加倍。因此,當K≥10時,利用K值改善分離度并不是一種明智的舉措。
圖4分離案例:K=10(上圖)與K=20(下圖)分離圖譜
選擇性α的應用
圖5分離度Rs與選擇性α之間的關系
分離度Rs與選擇性α之間的關系如圖5所示。而選擇性α的計算公式如下所示:
α=k2/k1
k1—色譜峰1的保留因子,k2—相鄰色譜峰2的保留因子
由圖可知,當選擇性1≤α≤2時,通過改變α值,分離度都能得到極大的改善。當選擇性α≥6時,通過改變α值,分離度Rs得到的改善相對變小。比較圖2、圖3及圖5縱坐標分離度Rs數值可知,影響分離的三要素中,選擇性α對分離的影響是最大的。即使選擇性α的微小改變,也能帶來分離度Rs的巨大改變。所以,選擇性α是改善分離度Rs的最有效方法。
實際工作中,對于選擇性α我們所用到的區域一般都是1≤α≤2的區域。為什么應用僅僅在此區域內呢?筆者用以下案例為大家解讀。色譜分離中,一般保證溶質的K介于1≤K≤10區間內。假設某物質分離條件為4.6*250mm,5um的色譜柱,流速為1.0ml/min,此時t0≈2.5min。當某物質保留因子K1=1,若α=2,則相鄰物質K2=2,此時兩物質的保留時間分別為t1≈5.0min, t2≈7.5min,這種情況下,二者已經完全分離。因此選擇性α>2時,分離度Rs已經滿足要求,不必再改善分離。所以,選擇性α在1≤α≤2的區域才有改善的必要。
分離條件對三要素的影響
以上部分,我們對分離度Rs與塔板數N,保留因子K,選擇性α之間的關系進行了論述。那么方法開發過程中,如何改善這三要素呢?通過圖6我們可以找到具體的控制措施。
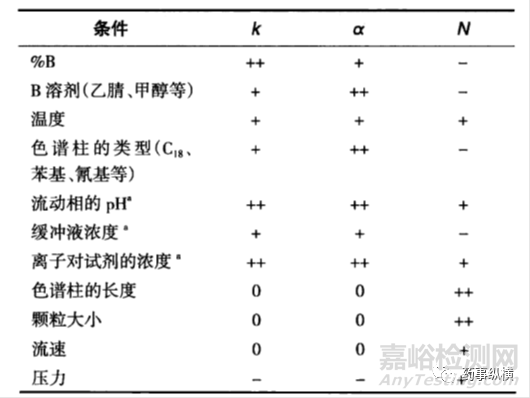
圖6分離條件對塔板數N,保留因子K,選擇性α的影響
++—主要影響,+—次要影響,-—相對影響較小,0—沒有影響,a— 對于可電離的溶質分子來說。
由圖6可知,塔板數N受影響條件較多,其中色譜柱長度和顆粒大小是影響塔板數N的主要條件,其具體計算公式前文也已經有論述,其他條件對塔板數N的影響相對較小。保留因子K主要影響因素包括有機相比例B%,流動相pH以及離子對試劑濃度。對于不可電離的物質而言,流動相pH以及離子對試劑濃度對保留因子K就不再是主要影響因素。選擇性α的主要影響因素為溶劑種類、色譜柱類型、流動相pH以及離子對試劑濃度,其他條件影響相對略小。當然有些分離條件對三要素的影響并不是孤立的,比如流動相pH,在改變保留因子K的同時也改變了選擇性α。因此,當我們明白分離條件對塔板數N,保留因子K,選擇性α的影響大小之后,后期開展工作才會有的放矢,更加高效。
以上便是筆者對分離度Rs與塔板數N,保留因子K,選擇性α之間的關系進行的解讀,鑒于筆者能力有限,若有不當之處,敬請各位讀者指正。
參考文獻:
1.《現代液相色譜技術導論》
2.《HPLC teaching assistant English v1.3》
3.《實用高效液相色譜法的建立》
4.《Count the Cost, Part I: Increasing Resolution byIncreasing Column Efficiency》
5.《Count the Cost, Part II: Increasing Resolution byIncreasing Retention》
6.《Count the Cost, Part III: Increasing Resolution byChanging Selectivity》