您當前的位置:檢測資訊 > 實驗管理
嘉峪檢測網 2017-09-05 16:04
問題:
某實驗室的一個流量計外送檢定,檢定結果為:10m3/h的點,示值誤差:-0.4%;2m3/h的點,示值誤差:0%,實際測試過程中流量為4m3/h,那么應該報告的流量結果為多少?
我們提供一種比較實用的方法:拉格朗日插值法,可以有效解決上述問題。
1、線性插值
插值是函數逼近的一種最簡單的重要方法,在數據處理中有著廣泛的應用,利用插值法可以通過函數在有限個點上的取值情況估算出在其它點上的函數值。


2、二次插值和n次插值
一般地,在我們的實際工作中,檢定證書(校準報告)都會提供多個點的誤差情況,此時,就需要用到二次拉格朗日插值多項式(3個點)或者n次拉格朗日插值多項式(更多個點)。而且,由于二次以上的函數圖形表現為曲線,更光滑,更美觀,也更能逼近真實的f(x)。
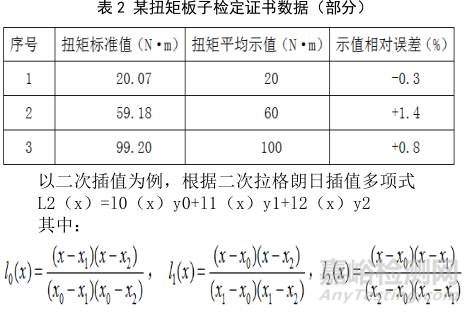
根據一次和二次插值多項式,我們推廣二次拉格朗日插值的表達式,可得n次拉格朗日插值多項式:
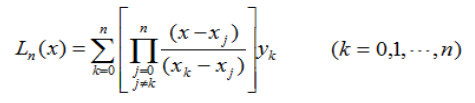
3、分段線性插值
3.1、高次插值多項式的陷阱
從圖1、圖2來看,似乎插值節點越多,誤差越小,函數逼近越好。然而,事實并非如此。

根據n次拉格朗日插值多項式,分別取前4個,前5個和全部6個校準點的數據繪制校準曲線,圖形分別如圖3、圖4、圖5所示。
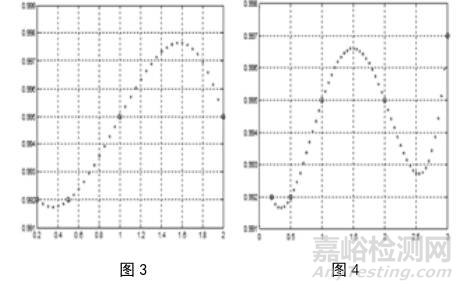

可以從圖5發現,在流量位于4.5m3/h左右時,曲線產生了大幅的振蕩,對應的修正因子顯然不能采信。如果進行多次類似試驗,那么我們能總結這么一個規律:當節點數大于5,且數據呈現出非線性時,節點加密不但不會逼近真實函數f(x),反而會導致了誤差的增大,這一現象被稱為Ronge現象。Ronge現象否定了利用高次插值多項式提高逼近精度的想法,事實上,一般使用n次拉格朗日插值多項式時,其節點不大于5個。
3.2分段線性插值
由圖3我們可知,當遇到校準點大于5個的檢定證書(校準報告)時,我們就不能采用高次插值多項式的方法去繪制校準曲線。怎么才能對付這個問題?驀然回首,利用最簡單的線性插值法就可以有效地解決這個困難。將每兩個相鄰的校準點作線性插值,然后將這些線段相連,即為分段線性插值函數的圖形描述。其公式可以描述為:

3.3、 Hermite 插值和三次樣條插值
分段線性插值在解決多校準點的情況下,具有簡單快速的優點。但是,其圖形表現為折線而非曲線,從函數逼近上看并非完美。就這個角度而言,Hermite 插值法和三次樣條插值法更具有優勢。Hermite 插值是利用未知函數 f(x)在插值節點上的函數值及導數值來構造插值多項式的,而三次樣條插值為了具有更好的光滑性,還要用到二階導數。
例如,表 3 所給出的測試數據用 Hermite 插值法和三次樣條插值法,在 Matlab 上繪制出的圖形分別如圖 7、圖 8 所示。
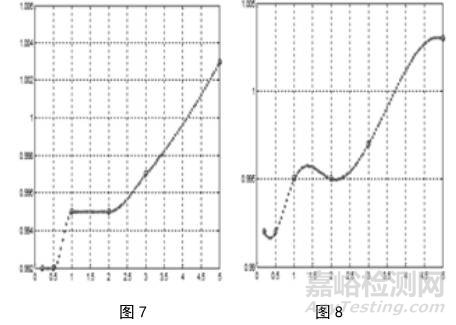
一般情況,Hermite 插值和三次樣條插值的圖形更光滑,逼近效果更好。但由于計算過程過于繁瑣,一般情況下,還是用分段線性插值法更具有可操作性,它所提供的修正因子已具有足夠的準確度和有效性。

來源:實驗室ISO17025


