對航空裝備在熱帶海洋大氣環(huán)境下服役時對金屬材料大氣腐蝕預測的需求��,提出了主成分分析法(PCA)優(yōu)化的BP神經(jīng)網(wǎng)絡(BPNN)和廣義回歸神經(jīng)網(wǎng)絡(GRNN)模擬熱帶海洋大氣腐蝕預測模型。研究結果表明,PCA可以很好地對原始數(shù)據(jù)的進行特征提取,降低樣本集的維度��。PCA-BPNN和PCA-GRNN模型的擬合優(yōu)度與預測精度沒有明顯的相關關系��。與PCA-BPNN相比���,PCA-GRNN的預測精度高���、穩(wěn)定性更好,這為模擬熱帶海洋大氣腐蝕研究提供了新思路��,具有較好的借鑒意義���。
引言
近年來�����,隨著我國南沙珊瑚熱帶建設從填海階段進入新的階段��,部署在沿海甚至熱帶地區(qū)的工業(yè)配套設施越來越多,例如船塢�����,機場����,海上石油平臺等。而當航空裝備在熱帶海洋大氣環(huán)境下服役時���,其材料不可避免地受到熱帶海洋大氣環(huán)境的影響,由于熱帶海洋大氣環(huán)境具有三高一強(高溫��、高濕��、高鹽及強太陽輻射)的環(huán)境特點���,航空裝備典型金屬材料的耐腐蝕性受到了極大的考驗���。近年來����,為了研究航空裝備鋁合金在熱帶海洋大氣環(huán)境下的腐蝕行為�����,相關研究人員開展了大量鋁合金材料在熱帶海洋大氣環(huán)境相關的自然暴曬試驗及實驗室加速試驗����,積累了大量的基礎試驗數(shù)據(jù)���,如何對這些基礎試驗數(shù)據(jù)進行有效利用以及如何利用現(xiàn)有數(shù)據(jù)推測未來變化趨勢或壽命規(guī)律�����,是航空裝備環(huán)境工程中亟需解決的問題����。
研究人員通過建立各種回歸模型來預測大氣腐蝕�,但大氣腐蝕影響因素眾多且作用復雜,使用回歸模型預測大氣腐蝕具有很大的局限性���。而人工神經(jīng)網(wǎng)絡是一種以現(xiàn)代神經(jīng)生物學為基礎,能夠模擬人腦神經(jīng)網(wǎng)絡結構和功能的一種計算結構���。它具有非線性映射能力、分布式信息存儲能力�����、大規(guī)模并行信息處理能力和自學習����、自組織、自適應能力��。隨著計算機行業(yè)的迅速崛起�,人工神經(jīng)網(wǎng)絡被廣發(fā)地運用在腐蝕與防護領域���,并取得了不少研究成果��。李強等通過BP神經(jīng)網(wǎng)絡建立了油氣管線腐蝕速率的預測模型��,并通過數(shù)值仿真模型試驗證明了BP神經(jīng)網(wǎng)絡建立的預測模型穩(wěn)定性好、預測精度高�����、使用效果良好����。靳文博等通過優(yōu)化后的廣義回歸神經(jīng)網(wǎng)絡建立了海底腐蝕管道的極限承載力的預測模型,并通過有限元計算,驗證了該模型的預測精度及使用穩(wěn)定性�����。X. Xia等使用人工神經(jīng)網(wǎng)絡模型預測不同微量金屬的添加對鎂合金耐腐蝕性能的影響���,研究結果表明�����,人工神經(jīng)網(wǎng)絡模型可以在一定測試范圍內準確預測材料的硬度和腐蝕速率�。Ling Ding等采用廣義回歸神經(jīng)網(wǎng)絡模型���,對9中不同理化性質的土壤中鋼材的腐蝕電位值和腐蝕電流密度進行了預測��。試驗結果表明���,GRNN模型的計算結果與試驗結果吻合好��,表明該模型能夠較好地預測鋼試件在不同土壤中的腐蝕活性����。
由于大氣腐蝕的環(huán)境影響因素較多,且各因素之間具有內在的關聯(lián)性����,直接采用收集到的數(shù)據(jù)進行建模��,會導致算法的性能和準確率降低��。因此,通過特征提取獲得能夠全面反映大氣腐蝕影響因素的少量參數(shù),具有重要的意義�。本文以典型航空材料某2000系鋁合金和某7000系鋁合金為研究對象��,通過主成分分析法對監(jiān)測的模擬熱帶海洋大氣腐蝕環(huán)境影響因素進行特征提取,通過BP神經(jīng)網(wǎng)絡以及廣義回歸神經(jīng)網(wǎng)絡構建了相應的預測模型,并對預測模型的預測精度進行了分析和研究�。
人工神經(jīng)網(wǎng)絡的構建
1�����、數(shù)據(jù)集的獲取
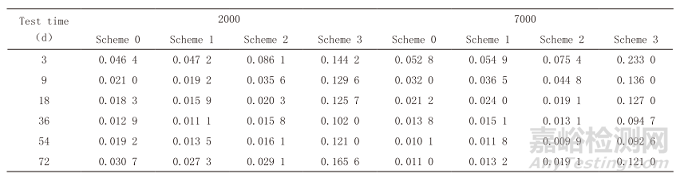
本論文通過本所之前試驗所獲得的數(shù)據(jù)作為數(shù)據(jù)集,詳細數(shù)據(jù)如表1所示。
表1 某2000系、某7000系鋁合金在不同方案加速試驗中的腐蝕速率
2���、BP神經(jīng)網(wǎng)絡的構建
BP人工神經(jīng)網(wǎng)絡(Back Propagation Neural Network, BPNN),一種導師型的學習算法,是人工神經(jīng)網(wǎng)絡(Artificial Neural Network, ANN)中最常用�����、最成熟的神經(jīng)網(wǎng)絡之一��,已被廣泛地運用于教學�����、科研和工業(yè)生產(chǎn)等領域。該網(wǎng)絡的主要特點是:信號前向傳播���,誤差反向傳播��。在前向傳遞中�,輸入信號從輸入層隱含層逐層處理��,直到輸出層�����。前一層的神經(jīng)元狀態(tài)只影響下一層神經(jīng)元狀態(tài)。如果輸出層得不到期望輸出�����,則轉入反向傳播����,然后根據(jù)預測誤差再來調整網(wǎng)絡權值和閾值,不斷循環(huán)從而使BPNN預測輸出不斷接近期望輸出�����。
2.1.樣本集預處理的構建
在BPNN中��,輸出量一般選擇構建模型需要預測的目標�,輸入量選擇對輸出量影響較大且相對容易檢測或提取的量���,且各種輸入量之間無相關或相關性較低����。在本論文中,輸出量選擇鋁合金的腐蝕速率����,輸入量選擇鋁合金的化學成分Cu含量、Mn含量�、Zn含量��、腐蝕加速試驗的試驗時間、pH值��、有無太陽輻射�����、有無珊瑚鹽��,其中,有無太陽輻射以及有無珊瑚鹽為語言變量,0代表無太陽輻射和無珊瑚鹽�,1代表有太陽輻射和有珊瑚鹽��。輸入量及輸出量如表2所示����。
表2 驗證樣本數(shù)據(jù)
通常�,收集的腐蝕影響參數(shù)越多,對腐蝕情況的描述就越全面�。但是�����,由于腐蝕影響因子之間具有內在的關聯(lián)性。收集的樣本數(shù)據(jù)會存在重疊數(shù)據(jù)����,導致在后期進行腐蝕預測時��,算法的性能和準確率降低。因此����,本論文使用主成分分析法對輸入數(shù)據(jù)進行特征提取��。
主成分分析法(Principle Component Analysis, PCA)是一種將多個指標化為少數(shù)互相無關的綜合指標的統(tǒng)計方法。它通過將原來指標重新組合成一組新的互相無關的幾個綜合指標來代替原來指標�����,同時根據(jù)需要從中取幾個較少的綜合指標盡可能多地反映原來指標的信息��。通過主成分分析能夠客觀地確定各指標的權重,避免主觀隨意性帶來的偏差,對多指標變量進行科學評價。
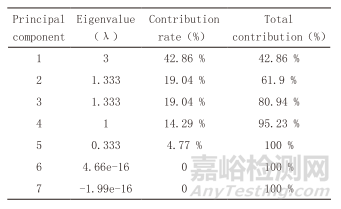
將表2中的數(shù)據(jù)進行主成分分析���,獲得初始和累積特征值和主成分系數(shù)矩陣,表3為初始和累積特征值。
表3 初始和累積特征值
以往試驗研究表明���,累積貢獻率>85%時,就能保證降維時丟失的信息量足夠少。因此選取前4個主成分為腐蝕影響因素���。相應的主成分系數(shù)矩陣如表4所示。
表4 主成分系數(shù)矩陣
由表4和PCA重組原理可計算得到重組后的數(shù)據(jù)序列,設前4個主元分別為����,結果如表5所示����。將表5中序號為6�、12、18、24����、30���、36���、42���、48的樣本數(shù)據(jù)作為模型的驗證樣本�,其余的作為模型的建模樣本����。
表5 PCA重構的樣本數(shù)據(jù)
2.2.網(wǎng)絡結構設計和網(wǎng)絡訓練
采用3層BP神經(jīng)網(wǎng)絡結構�,第一層為輸入層,中間層為隱含層����,第三層為輸出層����。輸入層有4個節(jié)點�,分別對應E1、E2�、E3�����、E4。隱含層選用10個節(jié)點�。網(wǎng)絡隱含層中的神經(jīng)元均采用tansig型變換函數(shù)�����,輸出層中的神經(jīng)元均采用logsig型變換函數(shù)��,訓練函數(shù)使用TrainLM函數(shù)。
3、廣義回歸神經(jīng)網(wǎng)絡的構建
廣義回歸神經(jīng)網(wǎng)絡(Generalized Regression Neural Network, GRNN)是一種基于非線性回歸理論的前期反饋神經(jīng)網(wǎng)絡,其核心是徑向基網(wǎng)絡�,具有訓練速度快�����、全局收斂性好、調節(jié)參數(shù)少等優(yōu)點。
GRNN的使用樣本集與BPNN使用的樣本集一致。當訓練樣本確定后���,其網(wǎng)絡結果以及各神經(jīng)元之間的連接權值也隨之確定,影響GRNN輸出的唯一因素是光滑因子。為了說明不同光滑因子對腐蝕預測結果的影響����,本論文分別使用光滑因子為0.1、0.2����、0.3���、0.4���、0.5�、0.6��、0.7����、0.8����、0.9、1.0的廣義回歸神經(jīng)網(wǎng)絡來進行預測�����,并對預測結果進行分析�����。
4����、模型評估方法
為驗證模型建模效果�����,選用擬合優(yōu)度(Goodness of Fit, GF)指標來評估模型的擬合性能。計算公式為:
選用平均絕對百分比誤差(mean absolute percent error, MAPE)指標來評估模型的預測性能。計算公式為:
選用相對誤差(Relative Error, RE)指標來評估模型預測值與實測值之間的差距���。計算公式為:
式中:
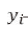 —測試樣本集的真實值;
—測試樣本集的真實值;
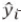 —預測值;
—預測值;
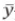 —測試樣本集的均值;
—測試樣本集的均值;
n—樣本集����。
GF越接近于1��,表明模型對訓練樣本的擬合程度越好;MAPE與RE越接近于0,表明預測的誤差越小,模型的預測效果越好。
結果對比與分析
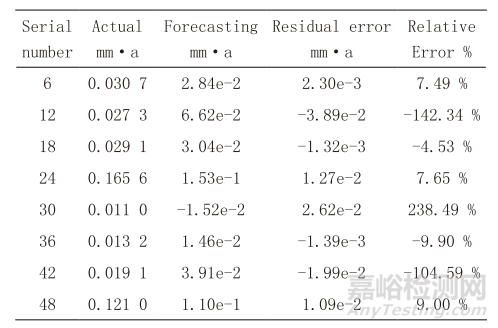
使用建模樣本數(shù)據(jù)進行人工神經(jīng)網(wǎng)絡的建模/訓練�,并將8組驗證樣本代入訓練/建模好的PCA-BPNN和PCA-GRNN模型進行驗證���。其預測結果如圖1����、圖2���、表6���、表7所示�。圖1為構建10次BPNN模型的GF和MAPE,由圖中可以看出,一方面, PCA-BPNN的GF和MAPE沒有表現(xiàn)出明顯的相關性�����,無法通過GF的高低來推出模型的預測精度。另一方面���,BPNN的MAPE較高,最低為60.91%���,最高高達136.54%。表6為MAPE為60.91%的PCA-BPNN模型預測結果�����,由表中可以看出�,8組驗證數(shù)據(jù)中�,有五組數(shù)據(jù)的相對誤差低于10%,但另外3組數(shù)據(jù)的相對誤差則超過了100%,這表明了該PCA-BPNN具有較好的預測精度���,但其穩(wěn)定性較差。
圖2為GRNN模型光滑因子Spread值分別為不同時的RE及MAPE,由圖中可以看出�����,PCA-GRNN模型的GF隨著光滑因子的增加而減弱��,這表明了光滑因子越大��,PCA-GRNN對建模樣本的擬合度則越差;MAPE隨著光滑因子的增加表現(xiàn)出先下降后上升的趨勢,當光滑因子小于0.5時��,其MAPE基本一致�,皆為31.26%,表現(xiàn)出較好且穩(wěn)定的預測性能;當光滑因子為0.8時��,其MAPE最低��,為29.49%�;這表明了PCA-GRNN模型與PCA-BPNN模型一樣�,其GF與MAPE并沒有表現(xiàn)出明顯的相關性。表7為光滑因子為0.8時,GRNN模型的預測結果,由表7中可以看出��,GRNN模型的相對誤差基本在(30%����,45%)區(qū)間內,還有兩個數(shù)值的相對誤差低于10%。因此����,PCA-GRNN模型的預測精度更高����,能夠更為準確地預估鋁合金在模擬南海熱帶大氣環(huán)境下的腐蝕速率��,預測結果更為可靠。
由圖1和圖2可以看出�����,構建了10次PCA-BRNN模型的MAPE最小值為60.91%���,最大值為136.54%����,而PCA-GRNN模型的MAPE都在30%左右。由表6和表7可以看出��,MAPE最低的PCA-BPNN模型的預測結果中�����,五組數(shù)據(jù)的RE低于10%����,三組數(shù)據(jù)的RE高于100%�,而MAPE最低的PCA-GRNN模型的預測結果中,僅兩組數(shù)據(jù)的RE低于10%�,其余數(shù)據(jù)的RE均在45%以內���。這表明PCA-GRNN模型的部分數(shù)據(jù)的預測精度低于PCA-BPNN�,但其預測精度的穩(wěn)定性遠優(yōu)于PCA-BPNN�����,因此���,PCA-GRNN比PCA-BPNN更加適合鋁合金模擬南海熱帶海洋大氣腐蝕的建模研究���。
圖1 BPNN模型的擬合優(yōu)度與平均絕對百分比誤差
表6 BPNN模型的預測結果
圖2 GRNN模型的擬合優(yōu)度與平均絕對百分比誤差
表7 GRNN模型的預測結果
結論
1)根據(jù)模擬熱帶海洋大氣環(huán)境的試驗條件��,確定了影響鋁合金腐蝕行為的腐蝕影響因素,并構建了相應的樣本數(shù)據(jù)���。使用PCA對原始樣本數(shù)據(jù)的特征進行提取,降低了樣本維度��,消除了變量間的重疊度����。
2)無論是PCA-BPNN還是PCA-GRNN,其模型的GF與MAPE沒有明顯的直接關系�����,并不能因為模型的高擬合優(yōu)度證明其具備高的預測精度�。當Spread值處于[0,1]區(qū)間時,PCA-GRNN的擬合優(yōu)度隨Spread值的上升而下降��,預測精度則表現(xiàn)出先上升后下降的趨勢�����。
3)相比于PCA-BPNN��,PCA-GRNN的MAPE較低且預測精度的穩(wěn)定性較強,基本都在30%左右�����,遠優(yōu)于PCA-BPMM模型的60%���,驗證了GRNN在鋁合金大氣腐蝕速率預測上的可行性及優(yōu)勢����,證明了GRNN模型對小樣本數(shù)據(jù)學習能力強���,調節(jié)參數(shù)少的優(yōu)勢��,將其用于預測腐蝕速率��,效果較好。
引用本文:
鄧俊豪�,陳荻云,張博,劉麗紅��,王榮祥��,龔雨荷.太PCA-ANN在典型航空材料鋁合金腐蝕數(shù)據(jù)預測中的應用[J].環(huán)境技術,2023,41(05):97-103+126.





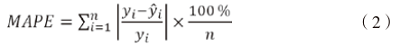

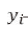 —測試樣本集的真實值;
—測試樣本集的真實值;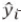 —預測值;
—預測值;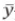 —測試樣本集的均值;
—測試樣本集的均值;