摘要:研究150~200Hz小振幅大預載下的橡膠動剛度預測,通過分析橡膠零部件的力位移曲線,得到橡膠零件在不同預載下的靜剛度,并通過試驗和分析得到不同頻率和應變水平下的動靜比,進而預測其動剛度。
關鍵詞:隔振率;動剛度;預載;應變;動靜比
隨著人們對汽車舒適性要求的提高,各大主機廠紛紛提出了動剛度的要求以提高懸置系統的隔振率。常見要求是全節氣門工況下動剛度小于一定數值,因此,對常用結構的動剛度預測在懸置開發過程中具有非常重要的意義。國內外已有很多學者利用試驗或計算方法或者兩者相結合的方法預測橡膠零部件的動剛度。在大變形下動態剛度與小變形情況有著不同的增加趨勢。Dzierzek建立了一種底盤襯套模型,可以模擬大范圍的靜載下和動載下的剛度和阻尼特性[1]。Y.H.Lee等假設一定頻率下的動靜比是常數,并利用橡膠試柱在一定頻率、一定應變水平下的試驗數據,來確定指定頻率和應變水平下的橡膠材料的動靜比,并利用該動靜比預測橡膠零部件的動剛度[2]。Dean、G等研究了小應變情況下炭黑填充橡膠的動態剛度在頻率、應變幅度和溫度方面的變化[3]。和法家、辛強等均采用測試試驗方法研究了預載、振幅和頻率對橡膠動剛度的影響[4,5]。楊俊鳳等研究了橡膠配方對橡膠動靜比的影響[6]。T. Shoyama等提出了PBERM方法測試高頻預剪和預壓下的材料動態特性參數,并指出預壓對動態性能的影響遠大于預剪,經驗模型的幾何相關性使橡膠零件幾何形狀改變時仍然需要做大量的試驗[7]。Hyun Seong Lee等使用有限元方法和經驗模型相結合的方法預測0~50Hz激勵頻率和不同振幅下的橡膠襯套的動剛度,大大減少了試驗次數和計算成本[8]。橡膠懸置有預載情況下的動態特性預測的挑戰在于:1)橡膠材料的粘彈性和非線性特點。2)預載導致的初始變形影響橡膠懸置的動態特性。3)動態特性的幾何相關性。本文通過試驗和仿真計算,研究兩種常用結構類型在300Hz以下小振幅大預載情況下動剛度的預測方法。
動剛度和頻率的相關性試驗和分析
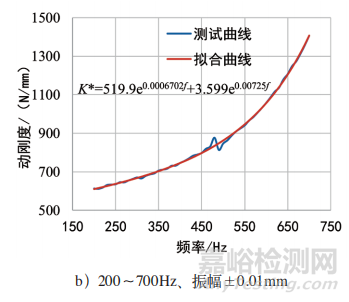
為了研究動剛度和頻率之間的一般關系,分別對樣件和典型零件進行振幅±0.01mm、頻率1~700Hz動剛度測試。圖1為試驗樣件模型,樣件中間的金屬板一端固定,另一端施加激勵力f。圖2為試驗用的十字筋襯套模型,零件外圈固定,在內芯處施加激勵振幅測試其動剛度。
圖 3 a 為樣件無初始應力在 1 ~ 700Hz 、振幅±0.01mm下動剛度和頻率的關系,符合雙指數關系。圖3b為零件無初始應力在200~700Hz、振幅±0.01mm下動剛度和頻率的關系,依然符合雙指數關系。圖3c為零件無初始應力在500~700Hz、振幅±0.01mm的測試曲線和擬合曲線。從擬合曲線來看,頻率越高,動剛度的增加速度越快。雖然動剛度和頻率之間符合雙指數函數關系,但是對于每一種材料、每一種形狀的零件,雙指數的參數必須通過試驗才能得到。為此將曲線分為不同頻段進行零件的動剛度分析。從曲線的走勢來看,低頻0~50Hz可以用一階線性擬合,即Kd/Ks(f)=af+b。其中Kd/Ks(f)為頻率f處的動靜比,b為橡膠材料10Hz或25Hz處的動靜比,a取決于零件使用的材料、幾何形狀和變形狀態,一般取值范圍為0.0012~0.0022,如圖4a所示。50~400Hz可以用一次或二次多項式擬合預測其動剛度,如圖4b和圖4c所示,均采用一次多項式來擬合有無預載下的動靜比和頻率的曲線。200~500Hz必須用二階或高階多項式擬合,如圖4d所示。對于500Hz以上的動剛度建議用雙指數函數擬合,通過試驗數據來得到高頻段的材料參數。


動剛度和預載的相關性
為研究動剛度和預載力間的關系,對兩個常用零件在固定頻率下進行有預載力的動剛度測試。圖5和圖6分別是進行試驗的零件1和零件2的模型,這兩種零件在5000N左右預載下具有較小的靜剛度和較低的動靜比。零件1和零件2的動靜比和預載力之間的關系曲線如圖7所示。從測試結果可以看出,預載力對動靜比的影響存在波動,但總體趨勢是預載越大,動靜比越大。
為更深入地研究預載對動靜比的影響,建立有限元模型,分析其在較大預載力下的應力應變分布。Hyun Seong Lee[8]等的研究表明,橡膠變形過程中壓應變對動特性的影響遠大于剪應變的影響。因此,在研究應變分布對動靜比影響時,取撞塊區域最大應變處的應變,圖8為零件1在3500N預載下的應力應變分布,圖9為零件2在7100N預載下的應力應變分布。




通過預載下動靜比和預載應變之間的關系得到如圖10所示的應變和動靜比之間的曲線。從圖10可以看出,在大變形下,動態剛度與小變形情況有著不同的增加趨勢,即大應變和小應變下動靜比的趨勢有很大不同:小應變下動靜比變化速度較小,大應變下動靜比變化速度很快。通過對比,零件1和零件2對應的拐點應變值不同,說明幾何形狀對動靜比的影響不可忽略。因此,對于同一種結構類型才可以使用應變來預測其大預載下的動靜比。
典型懸置零件動剛度預測
本文使用有限元方法預測零件的力位移曲線,橡膠本構模型選用3階Ogden模型。圖11為零件1和零件2的分析曲線和測試曲線對比。從對比結果來看,有限元分析可以很好地預測零件的曲線,即有限元可以較為準確地預測給定預載下的靜剛度。典型零件的動剛度預測流程如圖12所示。首先建立有限元模型,計算得到力和位移曲線及力和應變曲線,通過力位移曲線得到指定預載下的靜剛度,通過力應變曲線得到指定預載下的動靜比,預測的懸置動剛度即為靜剛度和動靜比的乘積。


結語
本文主要研究了0~700Hz大范圍內動靜比和頻率之間的關系,并指出不同范圍內的動靜比預測可以使用不同的擬合模型。此外還研究了動靜比和預載及其應變分布之間的關系,通過分析試驗數據得到不同預載下動靜比存在波動,但總體趨勢是預載越大動靜比也越大。并深入研究了應變和動靜比之間的關系,不同幾何形狀的零件應變和動靜比之間的關系有很大不同,目前通過應變和動靜比之間的關系預測動靜比僅可應用于同一種結構形式的零件。基于動靜比和頻率、動靜比和應變之間的關系,能夠預測文中提到的兩種常用結構類型在300Hz以下小振幅大預載情況下動剛度。基于本文的研究成果,為設計出滿足客戶要求的動剛度,需從結構和膠料兩方面考慮。1)對應預載下盡可能低的靜剛度。2)合理的結構使得選取的膠料硬度在50以內,或者選取 200Hz頻率下動靜比小于1.4的膠料。
參考文獻:[1] DZIERZEK S. Experiment-based modeling of cylindrical rubber bushings for the simulation of wheel suspension dynamic behavior [R].SAE,2000.[2] LEE Y H,KIM J S,KIM K J,et.al. Prediction of dynamic stiffness on rubber components considering preloads[J]. Mat.-wiss. u. Werkstofftech,2013,44(45).[3] DEAN G,DUNCAN J,JOHNSON A. Determination of non-linear dynamic properties of carbon-filled rubbers[J]. Polymer Test. 1984,4(2–4),225–249.[4] 和法家,盧曦. 某橡膠減震器動剛度特性試驗[J].試驗室研究與探索,2014,33(3):41-44.[5] 辛強,陳俠,王志懷. 動力總成懸置靜、動剛度的測試研究[J].汽車零部件,2016(5):79-81.[6] 楊俊鳳,周相榮,丁煒.橡膠減振器的動靜比影響因素[J].噪聲與振動控制,2013,33(6):201-206.[7] SHOYAMA,FUJINMOTO K. Direct measurement of high-frequency viscoelastic properties of predeformed rubber[J],Polymer Testing,2018,67:399–408.[8] LEE Hyun Seong,SHIN Jae Kyong,MSOLLI Sabeur,KIM Heung Soo. Prediction of the dynamic equivalent stiffness for a rubber bushing using the finite element method and empirical modeling[J]. International Journal of Mechanics and Materials in Design.2019,15(1):77-91.
















