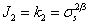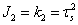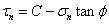屈服準則表示在復雜應力狀態下材料開始進入屈服的條件,它的作用是控制塑性變形的開始階段。屈服條件在主應力空間中為屈服方程。
一、幾種常用的屈服準則
五種常用的屈服準則,它們分別是Tresca準則,Von-Mises準則 ,Mnhr-Coulomb準則,Drucker Prager準則,Zienkiewicz-Pande準則。其中后三種適用于混凝土和巖土材料的準則。
1、Tresca屈服準則
當最大剪應力達到一定數值時,材料開始屈服。這就是Tresca屈服條件,也稱為最大剪應力條件。
規定σ1≥σ2≥σ3時,上式可表示為:
如果不知道σ1、σ2、σ3的大小順序,則屈服條件可寫為:
換言之當變形體或質點中的最大切應力達到某一定值時,材料就發生屈服。或者說,材料處于塑性狀態時,其最大切應力是一個不變的定值,該定值只取決于材料在變形條件下的性質,而與應力狀態無關。所以Tresca屈服準則又稱為最大切應力不變條件。
這種模型與靜水壓力無關,也不考慮中間應力的影響。在平面上屈服條件為一個正六邊形,在主應力空間內,屈服曲面為一個正六面柱體。
Tresca屈服準則不足之處就是不包含中間主應力,沒有反映中間主應力對材料屈服的影響。
2、Mises屈服準則
當與物體中的一點應力狀態對應的畸變能達到某一極限值時,該點便產生屈服,其表達式為:
或
其中,k為常數,可根據簡單拉伸試驗求得:
或根據純剪切試驗來確定:
它所代表的屈服面是一個以空間對角線為軸的圓柱體,在平面上屈服條件是一個圓。這時有:
換言之當等效應力達到定值時,材料質點發生屈服,該定值與應力狀態無關。或者說,材料處于塑性狀態時,其等效應力是不變的定值,該定值取決于材料變形時的性質,而與應力狀態無關。Mises屈服準則的物理意義:當材料的單位體積形狀改變的彈性能達到某一常數時,質點就發生屈服。故Mises屈服準則又稱為能量準則。
3、Mnhr Coulomb準則
Tresca屈服條件和Mises屈服條件主要是對金屬材料成立的兩個屈服條件,但是這兩個屈服條件如果簡單地應用于巖土材料,會引起不可忽視的偏差。
針對此,Mohr提出這樣一個假設:當材料某個平面上的剪應力τn達到某個極限值時,材料發生屈服。這也是一種剪應力屈服條件,但是與Tresca屈服條件不同,Mohr假設的這個極限值不是一個常數值,而是與該平面上的正應力σn有關,它可以表示為:
上式中,C是材料粘聚強度,Φ是材料的內摩擦角。這個函數關系式可以通過實驗確定。一般情況下,材料的內摩擦角隨著靜水應力的增加而逐漸減小,因而假定函數對應的曲線在σn-τn平面上呈雙曲線或拋物線或擺線。但在靜水應力不大的情況下,屈服曲線常用Φ等于常數的直線來代替,它可以表示為:
上式就稱為Mohr-Coulomb屈服條件。
設主應力大小次序為σ1≥σ2≥σ3,則上式可以寫成用主應力表示的形式
4、Drucker Prager準則
Drucker-prager屈服準則是對Mohr-Coulomb準則的近似,它修正了Von Mises 屈服準則,即在Von Mises表達式中包含一個附加項。其屈服面并不隨著材料的逐漸屈服而改變,因此沒有強化準則, 塑性行為被假定為理想彈塑性,然而其屈服強度隨著側限壓力(靜水應力)的增加而相應增加,另外,這種材料考慮了由于屈服而引起的體積膨脹,但不考慮溫度變化的影響。故此材料適用于混凝土、巖石和土壤等顆粒狀材料。
在主應力空間中,D-P屈服面為一曲面,其表達式為:
上式:f為塑性勢函數,I1(σij)為應力張量第一不變量,I2(Sij)為應力偏張量第二不變量,α,k為材料常數,是材料c,φ的函數,c,φ分別為材料的粘聚力和內摩擦角。
5、Zienkiewicz-Pande準則
Zienkiewicz-Pande 屈服準則是 Mohr-Coulomb 準則的改進,在 p-q 子午面和 π 平面上都是光滑曲線,不存在尖點,在數值迭代計算過程中易于處理,而且在一定程度上考慮了屈服曲線與靜水壓力的關系以及中主應力σ。是由Zienkiewicz、Pande 等學者在1977 年對 M-C 準則進行了修正與推廣時,形成了具有 3 種曲線形式的 Zienkiewicz-Pande 準則(簡稱 Z-P 準則)。這主要是考慮到M-C 準則在角點處存在奇異性,即其屈服曲線在 π 平面上有尖點,使得計算過程中出現奇異,特別在有限元迭代過程中,在尖角處無法處理的問題。
二、優缺點和適用范圍
1. Tresca準則
優點:當知道主應力的大小順序,應用簡單方便。
缺點:
(1) 沒有考慮正應力和靜水壓力對屈服的影響;
(2) 屈服面有轉折點,棱角,不連續。
適用:金屬材料
2. Mises屈服準則
優點:(1) 考慮了中主應力σ²對屈服和破壞的影響;(2) 簡單實用,材料參數少,易于實驗測定;(3) 屈服曲面光滑,沒有棱角,利于塑性應變增量方向的確定和數值計算。
缺點:
(1) 沒有考慮靜水壓力對屈服的影響;
(2) 沒有考慮單純靜水壓力p對巖土類材料屈服的影響及屈服與破壞的非線性特性;
(3) 沒有考慮巖土類材料在偏平面上拉壓強度不同的S-D效應。
適用:金屬材料
3. Mohr-Coulomb屈服準則
優點:
(1) 反映巖土類材料的抗壓強度不同的S-D效應對正應力的敏感性;
(2) 反映了靜水壓力三向等壓的影響;
(3) 簡單實用,參數簡單易測。
缺點:
(1) 沒有反映中主應力σ²對屈服和破壞的影響;
(2) 沒有考慮單純靜水壓力引起的巖土屈服的特性;
(3) 屈服面有轉折點,棱角,不連續,不便于塑性應變增量的計算。
適用范圍:巖石、土和混凝土材料
4. Drucker-Prager屈服準則
優點:
(1) 考慮了中主應力σ²對屈服和破壞的影響;
(2) 簡單實用,材料參數少,可以由C-M準則材料常數換算;
(3) 屈服曲面光滑,沒有棱角,利于塑性應變增量方向的確定和數值計算;(4) 考慮了靜水壓力對屈服的影響;(5) 更符合實際。
缺點:
(1) 沒有考慮單純靜水壓力p對巖土類材料屈服的影響及屈服與破壞的非線性特性;
(2) 沒有考慮巖土類材料在偏平面上拉壓強度不同的S-D效應;
適用范圍:巖石、土和混凝土材料
5. Zienkiewice-Pande準則
優點:
(1) 三種曲線在子午面上都是光滑曲線,利于數值計算;
(2) 在一定程度上考慮了屈服曲線與靜水壓力的非線性關系;
(3) 在一定程度上考慮了中主應力σ²對屈服和破壞的影響。
適用范圍:巖石、土和混凝土材料