物體的內部缺陷會對結構的力學性能產生顯著影響，如何有效檢測結構的內部缺陷是相關科研工作者致力研究的目標，國內外的許多學者都在開展有關結構內部缺陷的無損檢測研究。

 

常規的無損檢測技術包括目視檢測、超聲檢測、射線檢測、磁粉檢測、渦流檢測、滲透檢測等。選取合適的無損檢測方法可以有效地檢測結構的相關物理特性，從而對結構內部是否存在缺陷，以及缺陷的位置和類型進行判別。

 

超聲共振譜技術屬于超聲學的范疇，在20世紀60年代開始得到應用，主要應用于彈性常數的測量。該技術通過超聲換能器對結構進行掃頻激勵，檢測出結構的共振頻率，在已知結構尺寸、密度的情況下可以反演出材料的彈性常數。

 

當結構的內部存在裂紋或者缺陷時，結構的共振頻率就會發生改變，而超聲共振譜的共振峰對應的頻率即為結構的共振頻率，因此超聲共振譜可以反映出結構的變化，應用于結構的無損檢測。

 

傳統的超聲檢測技術包括超聲波脈沖回波和相控陣超聲法，而超聲共振譜技術目前應用案例較少。目前已有多種獲取結構共振譜的方法，如利用激光脈沖、磁場或接觸壓式電換能器。

 

同濟大學和東南大學的研究人員采用接觸式壓電換能器來獲取共振譜。以鋁制立方體結構為研究對象，通過有限元仿真研究結構內部缺陷對固有頻率以及超聲共振譜的影響，從而證明超聲共振譜可以應用于結構的無損檢測。并通過試驗判斷有限元仿真所得到的超聲共振譜與試驗測得的超聲共振譜的一致性，以驗證有限元仿真的準確性。最后比較試驗測量的有缺陷結構和無缺陷結構的超聲共振譜，驗證了基于超聲共振譜判斷結構是否存在缺陷的可行性。

 

超聲共振譜

 

一個彈性體在自由邊界條件下具有多個共振頻率，其共振頻率本質上為彈性體的固有屬性，只依賴于彈性體的幾何形狀、密度、彈性模量。

 

當彈性體的形狀和密度已知的情況下，將待測彈性體的兩個對頂角用超聲換能器夾住，一側超聲換能器不斷更換激勵頻率進行掃頻激勵，另一側超聲換能器接收振動信號；掃頻完成之后，接收信號的超聲換能器將所采集到的信號繪制成超聲頻譜，這就是彈性體的超聲共振譜。

 

當彈性體受到的激勵頻率與自身固有頻率相吻合時，超聲換能器會接收到一個幅值較大的信號，其幅值稱為共振峰值。因此，通過提取超聲共振譜的共振峰值對應的頻率便可以得到結構的固有頻率。

 

有限元仿真

 

1、有限元仿真過程

 

采用COMSOL有限元軟件進行仿真研究，建立的COMSOL有限元仿真模型如圖1所示，如圖1a所示，首先建立尺寸為8.1 mm×10 mm×18 mm的立方體鋁塊模型，該尺寸與后續試驗中所使用的試件尺寸一致。然后添加材料信息，設置材料參數，并賦予結構相應的材料參數。使用的材料均為鋁。

 

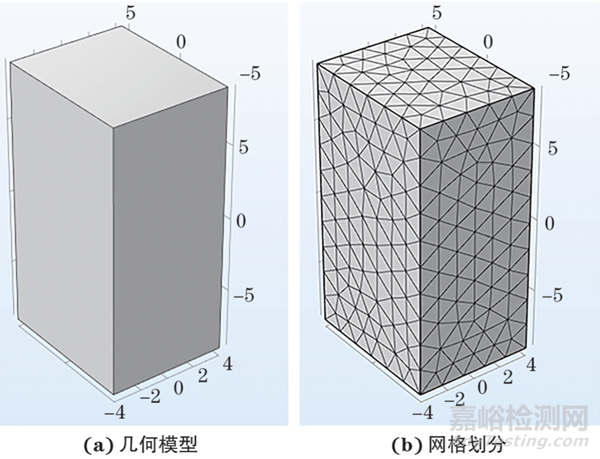
圖1 鋁塊的COMSOL有限元仿真模型

 

接下來進行物理場的設置，對于固有頻率的仿真，設置為“固體力學場”。根據超聲共振譜試驗的裝置設置，將自由邊界應用于結構的所有外表面，結構的中心點采用固定約束。最后對結構進行網格劃分，結果如圖1b所示。

 

通過COMSOL計算結構的固有頻率有兩種模式：特征頻率模式和頻域分析模式。

 

特征頻率模式是以某個頻率為中心，直接計算該頻率附近的固有頻率；頻域分析模式可以計算出給定頻率范圍內結構受到激勵后，結構位移的完整頻譜響應，這和實際情況更為接近。

 

由于試驗采取的是對頂角夾持，所以仿真時在立方體鋁塊的一個頂點（產生激勵的超聲換能器位置）添加點載荷，記錄對頂角（接收信號的超聲換能器位置）的位移大小，有限元仿真模型點位設置如圖2所示。然后繪制給定頻率范圍內的頻譜圖像，峰值所對應的頻率即為結構的固有頻率。

 

圖2 有限元仿真模型點位設置

 

2、結構共振頻率的計算

 

首先利用特征頻率模式計算結構的前30階固有頻率。在自由邊界條件下計算出的前6階固有頻率為剛性平移和剛性旋轉對應的固有頻率，故在分析時將其舍去，剩下的前24階固有頻率分布在70~260 kHz。

 

利用COMSOL的頻域分析模式，在70~270 kHz內，以25 Hz為步長進行掃頻，取對數后的超聲共振譜如圖3所示。

 

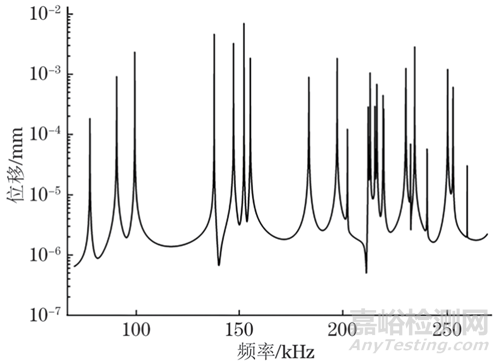
圖3 取對數后的超聲共振譜（仿真）

 

根據超聲共振譜的共振峰提取對應的固有頻率fRUS，其與特征頻率模式計算的固有頻率fcal的誤差e=(fRUS-fcal)/fcal×100%。

 

根據兩種模式計算的固有頻率可知，大部分固有頻率對于邊界條件不太敏感，通過超聲共振譜提取的固有頻率與直接計算的固有頻率偏差小于0.1%，但純彎曲模態和壓彎復合模態對邊界條件較為敏感，誤差會達到3%左右。因此，可以利用超聲共振譜有效地提取結構的固有頻率。

 

3、缺陷位置對超聲共振譜的影響

 

由于利用超聲共振譜測量法的前5階固有頻率相較于實際固有頻率通常有較大偏差，根據兩種模式計算的固有頻率與誤差也可以看出利用超聲共振譜測量的第2、3階固有頻率相較于直接計算的固有頻率有較大偏差，所以在分析時舍去前5階固有頻率。

 

出現這種偏差有可能是支架-試件耦合所致，即上述所提到的邊界條件的影響。為了研究缺陷位置對超聲共振譜的影響，對具有不同位置缺陷的結構進行仿真，得到各結構的超聲共振譜，并與無缺陷結構的超聲共振譜進行比較。

 

將缺陷的形狀設置為半徑0.6 mm的球體，以鋁塊的中心為原點，設置一系列不同位置的缺陷，缺陷的位置信息及幾何模型如圖4所示。

 

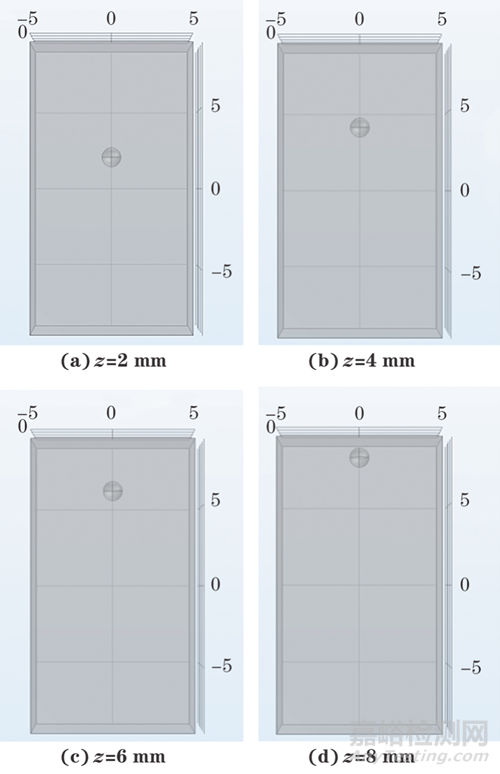
圖4 不同位置缺陷的幾何模型

 

用COMSOL頻域分析模式計算頻率為150~265 kHz的超聲共振譜。不含缺陷和含有不同位置缺陷結構的超聲共振譜（取對數后）如圖5所示。

 

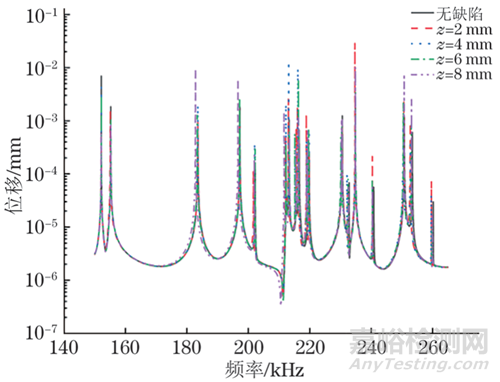
圖5 不同位置缺陷結構的超聲共振譜

 

由于超聲共振譜的頻域范圍很廣，很難直接觀察出不同結構的超聲共振譜共振峰的偏移情況，故通過超聲共振譜提取出每個結構的第6~24階固有頻率。并計算含缺陷結構與不含缺陷結構的同一階固有頻率的差值。

 

存在不同位置缺陷結構與無缺陷結構的第6~24階固有頻率差值曲線如圖6所示。存在不同位置缺陷結構與無缺陷結構的第7~14階固有頻率的差值隨模態階數的變化情況如表1所示。

 

圖6 存在不同位置缺陷結構與無缺陷結構的固有頻率差值曲線

 

表1 存在不同位置缺陷結構與無缺陷結構的固有頻率差值變化情況

 

 

↑表示該階差值比前一階差值大，↓表示該階差值比前一階差值小，- 表示該階差值與前一階差值一致。

 

根據圖6和表1可以看出，缺陷位于不同位置時，存在相同大小缺陷結構與無缺陷結構的第6~24階固有頻率的差值隨模態階數變化的趨勢不同，故可以根據固有頻率差值隨模態階數的變化趨勢確定缺陷所在位置。

 

4、缺陷大小對超聲共振譜的影響

 

為了研究缺陷大小對超聲共振譜的影響，對具有不同大小缺陷的結構進行仿真，得到各結構的超聲共振譜，并與無缺陷結構的超聲共振譜進行比較。

 

以鋁塊中心為原點，缺陷中心位于x=0 mm，y=0 mm，z=5 mm處，將缺陷形狀設置為半徑r分別為0.4，0.6，0.8，1 mm的球體，不同大小缺陷的幾何模型如圖7所示。

 

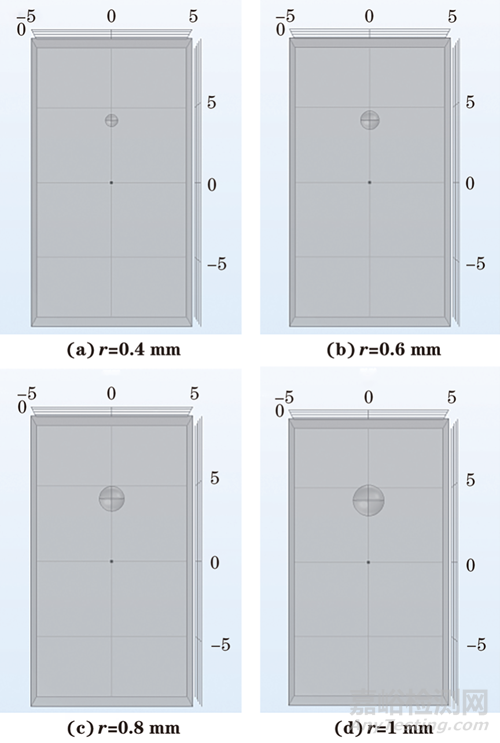
圖7 不同大小缺陷的幾何模型

 

無缺陷結構和存在不同大小缺陷的結構取對數后的超聲共振譜如圖8所示。

 

圖8 不同大小缺陷結構的超聲共振譜

 

存在不同大小缺陷結構與無缺陷結構的第6~24階固有頻率差值如圖9所示，可以觀察出當缺陷在同一位置時，存在不同大小缺陷結構與無缺陷結構的第6~24階固有頻率的差值隨模態階數變化的趨勢相似。

 

圖9 存在不同大小缺陷結構的固有頻率差值隨模態階數的變化曲線

 

此外根據圖9還可以觀察出，同一位置的缺陷直徑越大，含缺陷結構與無缺陷結構的同一階固有頻率的差值的絕對值越大，不同大小缺陷結構的6~24階模態固有頻率差值曲線如圖10所示，可以更為清晰地觀察出此規律。

 

圖10 不同大小缺陷結構的6~24階模態固有頻率差值曲線

 

結合上述結論可知：可以首先通過含缺陷結構的固有頻率與無缺陷結構的固有頻率的差值隨模態階數的變化趨勢來判斷結構缺陷的所在位置，再根據含缺陷結構的固有頻率與無缺陷結構的固有頻率的差值來判斷缺陷的大小，從而定位缺陷的位置與大小。故通過超聲共振譜來判斷結構缺陷的位置與大小具有可行性。

 

試驗驗證

 

1、試驗方案與儀器

 

超聲共振譜試驗裝置結構示意如圖11所示。試驗裝置包括激勵超聲換能器、接收超聲換能器、鎖相放大器、超聲換能器支架與夾具。

 

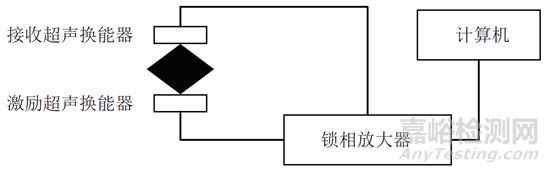
圖11 超聲共振譜試驗裝置結構示意

 

將制備的立方體試塊對角夾持在激勵超聲換能器和接收超聲換能器之間，通過鎖相放大器向激勵換能器輸入掃頻正弦信號，接收換能器接收掃頻激勵下的試塊位移響應信號，并輸出到鎖相放大器中。

 

當輸入的激勵信號接近試塊的固有頻率時，接收超聲換能器接收到的信號幅值會明顯增大，由此檢測出試塊的固有頻率。

 

2、試塊結構與尺寸

 

試塊1和試塊2的材料均為鋁，尺寸均為8.1 mm×10 mm×18 mm，其中試塊1沒有缺陷，試塊2在10 mm×18 mm的表面中心存在一個半徑為2 mm，深度為1 mm的圓柱形缺陷。試塊1和試塊2的幾何模型如圖12所示。

 

圖12 試塊1和試塊2的幾何模型

 

3、試驗數據和結果分析

 

利用搭建好的設備測量試塊1和試塊2的超聲共振譜。測量試塊1和試塊2所得的超聲共振譜與有限元仿真所得的超聲共振譜如圖13和圖14所示，頻域為150~270 kHz。

 

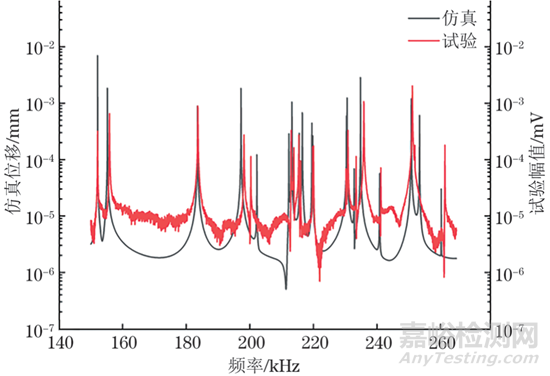
圖13 測量試塊1所得超聲共振譜與有限元仿真所得超聲共振譜

 

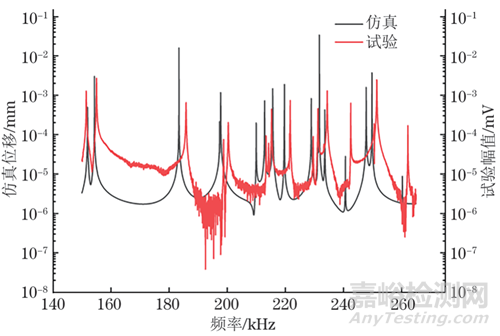
圖14 測量試塊2所得超聲共振譜與有限元仿真所得超聲共振譜

 

觀察圖13可以發現，測量試塊1所得與有限元仿真所得的超聲共振譜的大部分共振峰都是較為吻合的，但也存在一些有較大偏差的共振峰。

 

觀察圖14可以發現，測量試塊2所得與有限元仿真所得的超聲共振譜的共振峰均存在明顯偏差，試驗所得的共振峰相較于仿真所得的共振峰整體向右發生了偏移，但是兩者整體規律是一致的。

 

試驗測量與有限元仿真所得的超聲共振譜的誤差來源主要有以下幾方面：

 

(1) 試塊加工精度不高，導致試塊的結構不夠規則，是誤差的主要來源。

 

(2) 試塊的材料屬性與有限元仿真中設置的材料屬性存在差異。

 

(3) 實際的邊界條件與有限元仿真設置的邊界條件存在差異。

 

為了更細致地研究試驗所得與有限元仿真所得超聲共振譜的差異，根據試驗所得超聲共振譜提取試塊的固有頻率ftest，同時提取有限元仿真得到的超聲共振譜中的固有頻率fsim，并計算ftest相較于fsim的誤差，即e=(ftest-fsim)/fsim×100%。

 

試塊1仿真與測試所得的固有頻率誤差如表2和表3所示，可知試驗所得到的超聲共振譜提取出的固有頻率相較于有限元仿真結果中提取出的固有頻率，誤差大部分在1%以內，驗證了有限元仿真得到的超聲共振譜的準確性，故通過有限元仿真研究所得的結論也具有準確性。

 

表2 試塊1仿真與測試所得的固有頻率誤差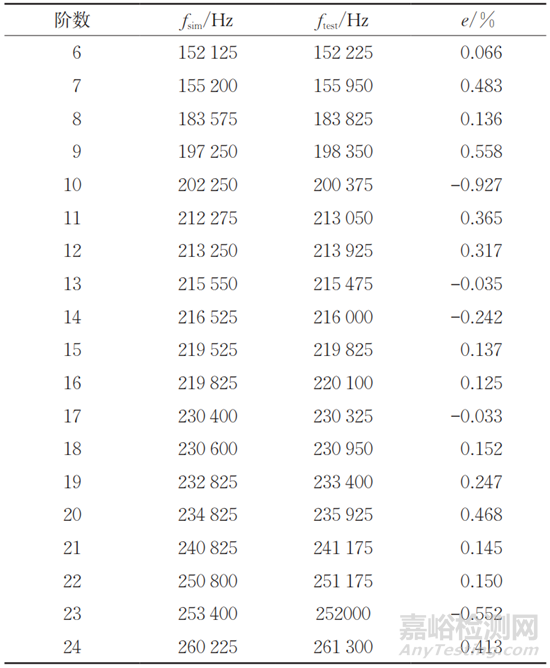

表3 試塊2仿真與測試所得的固有頻率誤差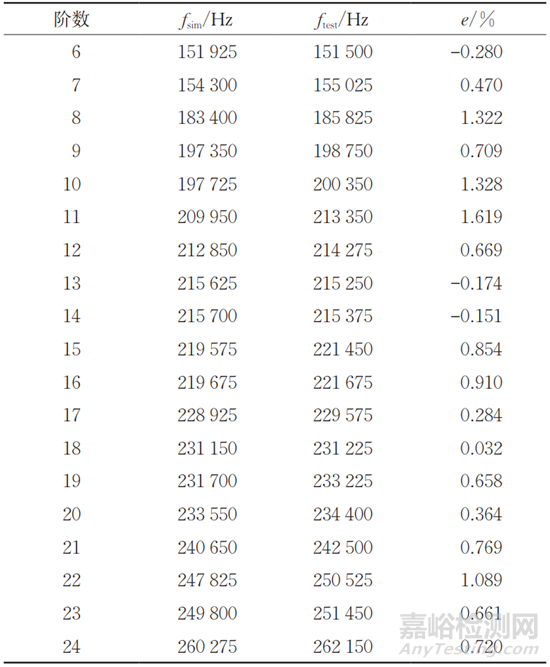

 

測量試塊1和試塊2所得的超聲共振譜如圖15所示，可見當結構存在缺陷時，超聲共振譜的共振峰相對于無缺陷結構的共振峰有明顯偏移，說明結構缺陷確實會對超聲共振譜產生影響，通過超聲共振譜來判斷結構是否存在缺陷是可行的。

 

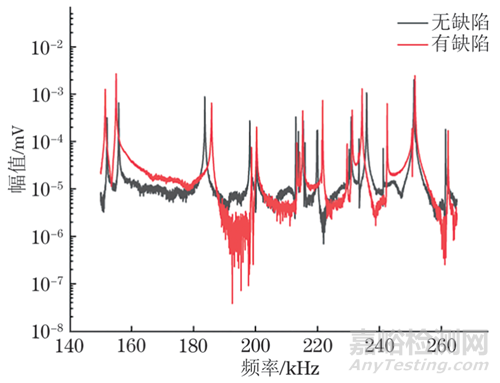
圖15 測量試塊1和試塊2所得的超聲共振譜

 

結語

 

(1) 通過COMSOL有限元仿真的特征頻率模式計算了結構自由振動的固有頻率，通過頻域分析模式仿真得到了超聲共振譜，并提取了共振峰對應的頻率，將兩組頻率進行比較，證明超聲共振譜能有效提取結構的固有頻率。

 

(2) 通過COMSOL有限元仿真的頻域分析模式仿真得到了立方體鋁塊的超聲共振譜，研究了當結構存在缺陷時固有頻率的變化，結果表明，當缺陷位于不同位置時，存在相同大小缺陷結構的固有頻率與無缺陷結構的固有頻率的差值隨模態階數變化的趨勢不同；當缺陷位于相同位置時，存在不同大小缺陷結構的固有頻率與無缺陷結構的固有頻率的差值隨模態階數變化的趨勢相似；當缺陷位于相同位置時，缺陷越大，含缺陷結構與無缺陷結構的同一階固有頻率的差越大。故可以通過超聲共振譜來判斷缺陷位置與大小。

 

(3) 通過試驗測量得到了無缺陷和有缺陷試塊的超聲共振譜，并與有限元仿真得到的超聲共振譜進行比較，驗證了有限元仿真獲得的超聲共振譜的準確性。

 

(4) 通過試驗測量得到的無缺陷和有缺陷試塊的超聲共振譜共振峰存在明顯差異，驗證了超聲共振譜可以用于判斷結構是否存在缺陷的結論。