前段制程（FEoL）常見的失效機理

1）與時間相關的電介質擊穿（TDDB）-- 柵極氧化物

2）熱載流子注入（HCI）

3）負偏壓溫度不穩定性（NBTI）

4）表面反轉（移動離子）

5）浮柵非易失性存儲器數據保持

6）局部電荷捕獲非易失性存儲器數據保持

7）相變（PCM）非易失性存儲器數據保持

 

后段制程（BEoL）常見的失效機理

1）與時間相關的電介質擊穿（TDDB）-- low k材質電介質/移動銅離子

2）鋁電遷移（Al EM）

3）銅電遷移（Cu EM）

4）鋁和銅腐蝕

5）鋁應力遷移（Al SM）

6）銅應力遷移（Cu SM）

封裝/界面常見的失效機理

1）因溫度循環和熱沖擊導致的疲勞失效

2）因溫度循環和熱沖擊導致的界面失效

3）因高溫導致的金屬間化合物和氧化失效

4）錫須

5）離子遷移動力學（PCB）--組件清潔度

 

本文對BEoL階段的與時間相關的電介質擊穿（TDDB）模型進行研究

 

BEoL TDDB研究的對象：

1）low k材質電介質

2）移動銅離子

 

low k材質電介質

雖然與時間相關的電介質擊穿（TDDB）是前段制程（FEoL）的一個關鍵可靠性課題，但TDDB不僅僅是柵氧化層的問題，如下圖所示用于后端制程（BEoL）應用的不同電介質的TDDB壽命趨勢與電場的關系。

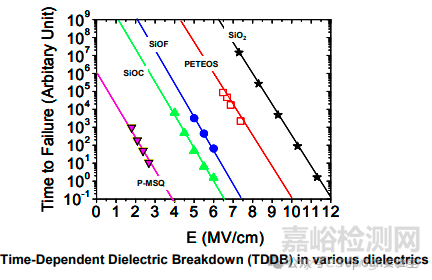
注：

1）等離子體增強TEOS（PETEOS）的結果引用自參考文獻[2]；

2）SiO2 的結果是針對柵氧化層；

3）SiOF、SiOC 和多孔 MSQ（P-MSQ）是low k材質互連電介質的示例；

4）對于BEoL電介質，其電介質可靠性隨著low k材質電介質常數的降低，擊穿強度呈現下降趨勢。

隨著low k材質電介質引入到互連堆疊，BEoL TDDB也成為了關鍵可靠性課題。與傳統的基于二氧化硅的BEoL電介質相比，low k材質能夠顯著改善RC性能（即減少電路延遲）；但在漏電和耐擊穿能力方面，比二氧化硅材質的柵氧化層要差得多。如上圖所示，low k材質電介質通常表現出較差的TDDB可靠性特性。

相鄰互連金屬層之間的金屬間電介質（IMD）間距正在接近幾十年前使用的柵氧化層的物理尺寸。因此，討論在電應力下電介質退化的物理模型類型很重要，特別是其與施加電場強度的相關性。

早期關于柵氧化層的工作表明，TDDB壽命模型與電場（E或1/E，參見前面關于柵氧化層TDDB的討論以比較模型《FEoL TDDB模型》）呈指數關系。E模型將TDDB描述為鍵斷裂模型，施加的電場可以拉伸硅-氧（Si-O）鍵，從而削弱它們并使它們發生熱斷裂。1/E模型遵循福勒-諾德海姆（F-N）傳導模型，電子穿過電介質因加速導致電介質碰撞發生電離損傷。

在正常使用條件下的電場強度范圍內，F-N傳導不顯著；同時，由于互連電極是金屬（其少數載流子貢獻可忽略不計），陽極空穴注入模型也不適用。因此，在較低電流下，low k材質的本征傳導模型可參考普爾-弗倫克爾（Poole-Frenkel）或肖特基（Schottky）模型，TDDB壽命基于這些傳導模型進行預估（建議遵循所謂的√E型模型）。

電場加速因子γ可用于表征在很寬電場強度范圍內的TDDB數據，γ因子根據研究結果總結得出為一個經驗值：不同模型中ln（失效時間）與電場的關系圖的斜率。可使用下面列出的方程標識：   

注：其中E是電介質中的電場，T是確定γ時的固定溫度，TTF被視為TDDB測試的特征失效時間。G和α分別是1/E和√E模型中的場加速參數。

場加速因子隨電場的變化可以從上述方程中預測。例如，E模型的場加速因子隨電場恒定，其他模型預測觀察到的場加速因子應隨電場強烈變化。

low k材質電介質有多種形式，由于工藝和集成方面的原因，行業的趨勢一直是采用基于氧化硅（SiOx）基質的材料。基于氧化硅的low k材質電介質已被證明在恒定電壓應力下具有較差的耐電壓擊穿強度和明顯更寬的失效分布，這些趨勢歸因于low k材質電介質中預先存在的缺陷，缺陷大致與low k材質電介質內的孔隙成正比。有趣的是，low k材質電介質TDDB仍然遵循在柵氧化層中發現的相同退化物理模型。即在105°C時，場加速因子γ≈4Naperians per MV/cm（約13eÅ的有效分子偶極矩）。

因low k材質電介質是通過有意在電介質中引入納米級孔隙而獲得的，所以材料的孔隙度是評估電介質電性能的一個重要特征。但從可靠性的角度來看，“孔隙”被認為是一個具有弱鍵的低極化率局部區域，在電應力下會引入電荷陷阱。滲流建模以及與孔隙成正比的缺陷假設可以解釋low k材質電介質擊穿強度的下降和更寬的失效分布。

由于low k材質電介質的BEoL處理非常復雜，BEoL工序必然會改變low k材質電介質的局部特性，因此在使用先進的low k材質材料時，仔細評估其可靠性裕度是BEoL成功處理和集成這些新材料的必要部分。low k材質電介質的可靠性不僅僅會影響金屬間的絕緣問題[下圖（a）]，還有金屬層間和柵極-金屬接觸的幾何結構也會收到影響。

另外，由于銅離子在電場下可移動，任何留下或允許銅離子進入電介質區域的缺陷都會使它們在金屬電極之間漂移，并對TDDB可靠性產生不利影響，水汽的存在也會對互連可靠性產生負面影響。

使用E模型的low k材質電介質TDDB壽命預估示例：

目標：

使用E模型計算low k材質電介質在使用條件下因TDDB導致失效的加速因子（AF）。

注：外推的基礎是從在加速失效的應力條件下獲得的測試結構壽命數據得出的。

假設條件：

1）正常使用條件為：50°C芯片溫度和0.3MV/cm的電場加速條件

2）加速條件為：125°C測試溫度和4MV/cm的電場加速條件

3）電場加速參數/因子，γ：4Naperians per MV/cm

4）表觀活化能Eaa：0.75eV

AF計算公式：

AF(TTFuse/TTFaccel)=exp[–γ(Euse–Eaccel)]*exp[(Eaa/k)(1/Tuse–1/Taccel)] 

 

假設條件代入計算：

 

AF=exp[–4.0/(cm/MV)(0.3MV/cm–4MV/cm)]*exp[(0.75eV/8.62x10–5eV/K)(1/(273+50)K–1/(273+125)K)]=2.7x106*1.6x102=4.3x108

結論：因此，正常使用壽命將比觀察到的加速應力壽命長約4×108倍。其中，2,700,000倍是由于電場加速引起的，因溫度加速只有160倍。

注：從上述例子可知，電場加速因子遠大于溫度加速因子。因此，可在正常使用溫度條件范圍增大電場強度進行加速壽命測試試驗。但加速壽命測試有一些必要的注意事項。

1）首先，在加速條件下（更高的施加電場和/或更高的溫度）進行測試可能會導致新的失效模型，這些模型并非與接近正常使用條件下的相關失效一致（例如，low k材質電介質中的銅離子在高于200°C時明顯變得可移動）；

2）其次，在加速條件下高度活化的缺陷（例如，游離銅）的存在會極大地扭曲壽命預測，盡管在這種條件下檢測到它們可以被視為進一步改進工藝的指標；

3）最后，測試結構的面積通常比實際器件中的互連面積小得多。

 

移動銅離子

如在影響器件功能的移動離子部分所提到的《移動離子失效模型》，在適度電場（≤1.0MV/cm）和溫度（~100°C）條件下，鋰、鈉和鉀之類的堿金屬元素在SiO2之類的電介質中特別容易移動。

隨著銅金屬化成功集成到后段制程（BEoL）中，在電偏壓下的移動銅離子是一個更嚴峻的問題。例如，溝槽/過孔金屬阻擋層或溝槽電介質阻擋層對銅離子擴散的阻擋完整性喪失或者存在與銅相關的腐蝕缺陷，都可能導致BEoL的絕緣電介質可靠性大幅下降。通常，電場下的銅離子漂移導致互連的TDDB問題想比半導體器件中的表面反轉（移動離子）更是一個問題。對于基于銅的互連金屬，這種故障模型的機理是兩個金屬電極之間的局部low k材質電介質形成的金屬短路橋，如下圖所示。

注：在沉積覆蓋電介質之前，對銅金屬化進行化學機械拋光（CMP）和清洗可能會留下銅離子缺陷，這些缺陷未被阻擋材料完全與low k材質電介質隔絕。在施加的電應力條件下，銅離子可以穿過電介質區域發生漂移，導致金屬間電介質（IMD）過早失效。嚴重的缺陷會對觀察到的TDDB可靠性產生負面影響。

Cu+離子可以通過增加Si-O鍵的局部電場來催化正常的Si-O鍵斷裂過程：Cu+離子將通過產生局部點缺陷對TDDB產生不利影響，這種點缺陷的產生在概念上類似于柵氧化層中的“空穴捕獲”--增強Si-O鍵周圍的局部電場，Si-O鍵斷裂最終導致low k材質電介質失效。

對于銅離子導致low k材質電介質失效確切作用以及在何種濃度下銅離子漂移會驅動low k材質電介質擊穿模型目前還沒有達成共識。但很明顯的是，充分遏制銅離子對于確保互連可靠性以防止電介質過早擊穿和進行電介質可靠性評估至關重要。如果阻擋層的遏制銅離子失敗，那么與大量銅離子漂移相關的大規模缺陷將以兩種方式影響電介質的可靠性：

1）隨著銅離子進入電介質并增加局部電場，有效電介質間距會逐漸減小；

2）銅離子漂移導致金屬橋接缺陷，使兩個電極短路。

low k材質電介質中可移動銅離子的漂移最終橋接。可移動離子通量由電場強度和溫度控制。因此，失效時間（TTF）的公式如下：

如果電場關閉并且對器件進行烘烤（即無偏壓烘烤），則離子電流 Jion 有可能改變方向（反向擴散），器件可能會表現出一定程度的恢復，稱為“失效烘烤恢復”；然而，在BEoL中，遷移的金屬陽離子也很可能與來自陰極的電子重新結合，隨后“沉積”形成永久短路通道，從而排除這種烘烤恢復的可能性。

 

將離子電流 Jion(x,t) 除以離子濃度 ρ(x,t)，可得到離子漂移的凈速度 Vion(x,t)。因此，失效時間的更明確表示為（電介質厚度）/ Vion(x,t)。

 

注：

 

1）首先，這個表達式是一個近似值。例如，如果發生了足夠的金屬沉積，那么在失效前的實際電介質間距可能小于標稱電介質厚度，并且在應力期間的實際標稱電場可能會隨時間增加。

2）其次，公式對所有溫度和電場都有效的假設是不正確的。例如，如果跳躍距離約為7Å，并且在電介質上施加0.2MV/cm的電場，公式在50°C時無效，但在250°C時有效。

通常，對于準確的加速因子確定和壽命預測，需要更復雜的漂移擴散表達式；然而，關于最有效的模型還沒有明確的共識。

 

在《移動離子失效模型》研究中，Stuart發現Na的活化能為0.75eV，而其他所有物質約為1.1eV或更高。對于銅擴散到電介質中，不同的作者根據測試結構、測試方法和所用電介質的類型，估算出不同的Eaa值（范圍從0.8eV到高達1.8eV。因此，對于本次討論，銅離子漂移擴散的Eaa選擇典型值1.0eV。

 

移動銅離子影響low k材質電介質TDDB壽命預估示例：

 

目標：

計算加速因子（AF），即AF=TTFuse/TTFaccel；通用模型（但不一定準確）。

假設條件：

1）正常使用條件為：50°C芯片溫度和1.0MV/cm的電場加速條件

2）加速條件為：250°C測試溫度和4MV/cm的電場加速條件

3）表觀活化能Eaa：1.0eV

失效判據：[Cu+n]=1018個離子/立方厘米

AF計算公式：

 

AF(TTFuse/TTFaccel)=(Jion,use/Jion,accel)-1*exp[(Eaa/k)(1/Tuse–1/Taccel)]

 

AF=(Eaccel/Euse)(Tuse/Taccel)*exp[(Eaa/k)(1/Tuse–1/Taccel)]

 

忽略反向擴散，Jion≈~（eE）*（ρDo/kT）

假設條件代入計算：

 

AF=(4.0MV/cm/1.0MV/cm)((273+50)K/(273+250)K)*exp[(1.0eV/8.62x10–5eV/K)(1/(273+50)K–1/(273+250)K)]=4.0*0.6176*9.223x105=~2.3x106

結論：電場是一個低加速因子，溫度是一個高加速因子。因此如果BEoL存在大量銅離子污染，電場低加速導致TDDB失效會造成芯片運行一定時間（較長的時間）失效。

 

相關文獻：

1）R. Tsu, J.W. McPherson, and W.R. McKee, “Leakage and Breakdown Reliability Issues Associated with Low-k Dielectrics in a Dual-Damascene Cu Process,” IEEE International Reliability Physics Symposium Proceedings, 2000, pp. 348-353. 

 

2）J. Noguchi, T. Saito, N. Ohashi, H. Ashihara, H. Maruyama, M. Kubo, H. Yamaguchi, D. Ryuzaki, K. Takeda, and K. Hinode, “Impact of Low-k Dielectrics and Barrier Metals on TDDB Lifetime of Cu Interconnects,” IEEE International Reliability Physics Symposium Proceedings, 2001, pp. 355-359.

 

3）E.T. Ogawa, J. Kim, G.S. Haase, H.C. Mogul, and J.W. McPherson, “Leakage, Breakdown, and TDDB Characteristics of Porous Low-K Silica-Based Interconnect Dielectrics,” IEEE International Reliability Physics Symposium Proceedings, 2003, pp. 166-172. 

 

4） G.H. Haase, E.T. Ogawa, and J.W. McPherson, “Breakdown Characteristics of Interconnect Dielectrics,” IEEE International Reliability Physics Symposium Proceedings, 2005, pp. 466-473. 

 

5）J. McPherson, “Determination of the nature of molecular bonding in silica from time-dependent dielectric breakdown data,” Journal of Applied Physics, Vol. 95, Issue 12, 2004, pp. 8101-8109 

 

6）J. Kim, E.T. Ogawa, and J.W. McPherson, “A Statistical Evaluation of the Field Acceleration Parameter Observed During Time Dependent Dielectric Breakdown Testing of Silica-Based Low-k Interconnect Dielectrics,” IEEE International Reliability Physics Symposium Proceedings, 2006, pp. 478-483.

 

7）J. Suñe, D. Jimenez, and E. Miranda, “Breakdown Modes and Breakdown Statistics of Ultrathin SiO2 Gate Oxides,” Internation Journal of High Speed Electronics and Systems, Vol. 11, No. 3, 2001, pp. 789-848. 

 

8）J.W. McPherson, R.B. Kamankhar, and A. Shanware, “Complementary model for intrinsic timedependent dielectric breakdown in SiO2 dielectrics,” Journal of Applied Physics, Vol. 88, Issue 9, 2000, pp. 5351-5359. 

 

9）W. Wu, X. Duan, and J.S. Yuan, “A Physical Model of Time-Dependent Dielectric Breakdown in Copper Metallization,” IEEE International Reliability Physics Symposium Proceedings, 2003, pp. 282-286. 

 

10）J. Noguchi, N. Miura, M. Kubo, T. Tamaru, H. Yamaguchi, N. Hamada, K. Makabe, R. Tsuneda, and K. Takeda, “Cu-Ion-Migration Phenomena and its Influence on TDDB Lifetime in Cu Metallization,” IEEE International Reliability Physics Symposium Proceedings, 2003, pp. 287-292. 

 

11）M.M. Eissa, D.A. Ramappa, E. Ogawa, N. Doke, E. M. Zielinski, C.L. Borst, G. Shinn, and A.J.McKerrow, “Post-Copper CMP Cleans Challenges for 90 nm Technology,” Advanced Metallization Conference Proceedings, 2004, pp. 559-570. 

 

12）F. Chen, K. Chanda, J. Gill, M. Angyal, J. Demarest, T. Sullivan, R. Kontra, M. Shinosky, J. Li, L. Economikos, M. Hoinkis, S. Lane, D. McHerron, M. Inohara, S. Boettcher, D. Dunn, M. Fukasawa, B.C. Zhang, K. Ida, T. Ema, G. Lembach, K. Kumar, Y.Lin, H. Maynard, K. Urata, T. Bolom, K. Inoue, J. Smith, Y. Ishikawa, M. Naujok, P. Ong, A. Sakamoto, D. Hunt, and J. Aitken, “Investigation of CVD SiCOH Low-k Time-dependent Dielectric Breakdown at 65nm Node Technology,” IEEE International Reliability Physics Symposium Proceedings, 2005, pp. 501-507. 13）N. Suzumura, S. Yamamoto, D. Kodama, K. Makabe, J. Komori, E. Murakami, S. Maegawa, and K. Kubota, “A New TDDB Degradation Model Based On Cu Ion Drift In Cu Interconnect Dielectrics,” IEEE International Reliability Physics Symposium Proceedings, 2006, pp. 484-489. 

 

14）J.R. Lloyd, C.E. Murray, S. Ponoth, S. Cohen, and E. Liniger, “The effect of Cu diffusion on the TDDB behavior in a low-k interlevel dielectrics,” Microelectronics Reliability, Vol. 46, 2006, pp. 1643-1647. 

 

15）S.-S. Hwang, S.-Y. Jung, J.-K. Jung, and Y.-C. Joo, “Study of Cu Migration-Induced Failure of Inter-Layer Dielectric,” IEEE International Reliability Physics Symposium Proceedings, 2006, pp. 673-674. 

 

16）K.N. Tu, J.W. Mayer, and L.C. Feldman, Electronic Thin Film Science, Macmillan Publishing, New York, 1992, p. 46.