鈦鈮系合金是新型高溫合金,具有優異的高溫強度和高溫抗蠕變性能,在航天、航空等高溫領域具有廣泛的應用前景,但作為結構零部件使用時,其硬度較低,導致其抗磨損、耐沖蝕等性能不足,因此需要通過表面改性等技術,來提高表面強度,改善合金表面的穩定性,進而提高零部件的使用壽命。合金的表面改性方法有:激光沖擊強化技術、表面熔覆技術、超音速熱噴涂技術、表面滲碳(氮)技術、雙金屬復合技術等。每種技術都有其自身的優缺點,需要對改性后的表面進行檢測和分析。對組織表征來說,材料的尺寸要求不高,一般都可實現微觀組織分析。受表面改性層(強化層)尺寸的限制,難以進行常規的力學性能測試,可進行的力學性能測試主要有納米壓痕測試、顯微硬度測試、劃痕測試等,都屬于局部測試。
顯微硬度測試是一種壓入法測試技術,通過將壓頭壓入材料表面,引起材料塑性變形,可反映材料抵抗塑性變形的能力。測得的硬度是一個綜合的物理性能指標,可反映材料的彈塑性、強韌性等一系列指標。壓痕斷裂力學中的相關理論認為,在壓頭壓入材料表面形成壓痕的過程中,壓痕周圍材料彈塑性形變引起的殘余應力是裂紋形成及擴展的驅動力。在平衡狀態下,斷裂韌性等于裂紋尖端的殘余應力場強度Kr。基于以上,可分析壓痕及裂紋的形貌和尺寸,再根據相關經驗公式,對材料的斷裂韌性進行評價。
朱建雷等研究人員采用顯微硬度儀對材料施加不同的載荷,以及在不同層內進行硬度測試,對表面強化層的硬度和裂紋形貌進行分析,研究了鈦鈮合金表面(TiNb)C強化層的顯微硬度及斷裂韌性。
1、 試驗材料與方法
將TiNb合金和HT300灰口鑄鐵通過緊密貼合的方式,在有氬氣氣氛保護的管式爐內進行等溫擴散處理(1150℃,8h)。利用碳原子的高擴散速率,在濃度梯度的驅使下,碳原子以擴散的方式進入TiNb合金表面,并發生原位固相擴散反應,在TiNb基體表面形成(TiNb)C強化層。
采用顯微硬度儀進行顯微硬度測試,試驗載荷為0.5,1,2,3,5,10N,載荷保持時間為10s。進一步采用掃描電鏡(SEM)觀察壓痕的形貌,測量壓痕的尺寸,再分析壓痕尖端裂紋的擴展方式,并測量裂紋的長度。
2、 試驗結果及討論
2.1 (TiNb)C強化層的組織結構
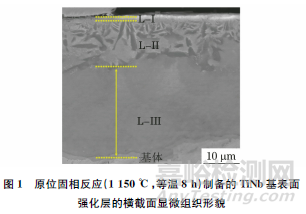
原位固相反應(1150℃,等溫8h)制備的TiNb基表面強化層的橫截面顯微組織形貌如圖1所示。
表面強化層由3層不同組織組成,形成致密的表面層狀結構:外層(L-I)、中間層(L-II)和內層(L-III)。每層組織的顆粒尺寸和形貌不同,但其主要物相均為(TiNb)C。L-I的厚度最薄,約為1μm~2μm,該層經過簡單磨拋處理就可去除;L-II內組織為微米級、米粒狀顆粒,平均層厚約為12.56 μm;L-III內組織為亞微米級、等軸狀顆粒,平均層厚約為24.92μm。
2.2 (TiNb)C強化層內的顯微硬度
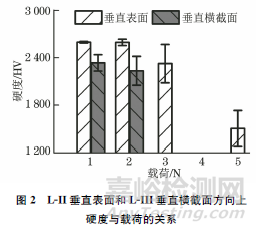
考慮到壓頭的尺寸效應以及壓痕的邊緣效應,受表面強化層厚度的影響,從垂直表面方向測量L-II的顯微硬度,從垂直橫截面方向測量L-III的顯微硬度。L-II垂直表面和L-III垂直橫截面方向上硬度與載荷的關系如圖2所示。由圖2可知:隨著測試載荷的增加,L-II的顯微硬度均高于L-III的顯微硬度。另一方面,隨著載荷的增加,L-II的顯微硬度和L-III的顯微硬度均逐漸降低。理論上,載荷越大,其他外在因素對硬度的影響越小,越能體現材料的真實硬度。受強化層厚度的影響,在提高載荷的同時,還需要考慮邊緣效應和基底效應。采用觀察壓痕的形貌、分析頂角裂紋和棱邊裂紋的擴展行為、測量裂紋長度等方法,可以確定合適的測試載荷,以獲得更接近實際的強化層硬度。
不同載荷下,L-II垂直表面方向的壓痕形貌及裂紋長度如圖3所示。在載荷為0.5N時,壓痕周圍裂紋較少,部分壓痕尖端還未有明顯的裂紋出現[見圖3a)]。隨著載荷的增加,壓痕頂角裂紋逐漸明顯且變長;同時,棱邊裂紋也逐漸明顯[見圖3d)],逐漸展現出相框裂紋的具體特征。相框裂紋的產生原因為高載荷下的高接觸應力和基底效應。當載荷提高至10N時,相框裂紋從棱邊延伸至壓痕中心點,呈龜裂狀。造成這種現象的主要原因是強化層和基體所組成的“硬殼-軟底”結構。在高應力下,硬殼將應力傳送至基體層,但軟質基體層強度不足,會發生較大的變形,進而導致表面強化層發生崩塌,形成如圖3f)所示的相框裂紋。此時,由于應力傳遞已經與基體關聯,并不能反映強化層的實際硬度。因此,結合壓痕形貌和裂紋擴展方式,可以判斷L-II測試時的臨界載荷為3N。由于當載荷為3N時,壓痕棱邊已經有相框裂紋形成,因此當載荷為2N時,所測顯微硬度為L-II的最可信硬度,其平均硬度為2594.13HV。

在不同載荷下,垂直橫截面方向L-III的壓痕形貌如圖4所示。經過多點測量和觀察,L-III壓痕的長度和尖端裂紋長度明顯大于L-II,而且L-III內的裂紋主要沿平行于表面的方向擴展。這主要是由強化層厚度引入的邊緣效應引起的。當載荷為0.5N時,L-III內壓痕的裂紋長度波動最小;當載荷為1N時,壓痕半長度的波動最小[見圖4b)]。進一步考慮到邊緣效應,當載荷為1N時,顯微硬度可作為L-III的最可信硬度,其平均硬度為2334.88HV。結果表明,雖然L-III組織中的晶粒具有更小的尺寸,為亞微米級,但是L-II呈現出較高的硬度。
2.3 強化層內的斷裂韌性
在斷裂韌性評級的精度和適應范圍方面,傳統壓痕法具有一定的局限性。對于薄膜類、涂層類以及表面類材料,特別是高脆、硬性表面強化層,由于材料本身尺寸的限制,壓痕法測量表面類或薄膜類材料的斷裂韌性具有方便、簡單等優勢,同時具有較高的精度。有關壓痕法計算斷裂韌性的經驗公式較多,且具有不同的應用范圍。同時,根據裂紋類型的不同,公式的選用也不同。大致可以分為中位裂紋和徑向裂紋。
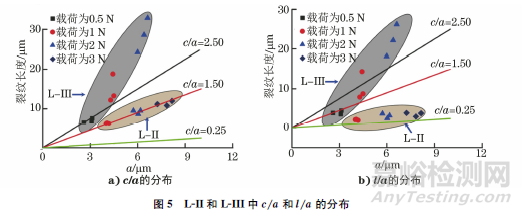
若想用壓痕法評價斷裂韌性,需先根據裂紋形貌判斷裂紋類型,再選擇適用的公式。在常規情況下,依據裂紋長度c(壓痕中心點至裂紋尖端的長度)或l(壓痕頂角至裂紋尖端的長度)與a(壓痕的半長度)的比值大小,可判斷裂紋的類型。對于多數材料:當c/a小于2.5時,為巴氏裂紋;當c/a 大于2.5時,為中位裂紋;當l/a小于1.5時,為巴氏裂紋;當l/a大于1.5時,為中位裂紋。L-II和L-III中c/a 和l/a 的分布如圖5所示。由圖5可知:在表面方向,隨著載荷的增加,L-II內c/a 均小于2.5,且l/a均小于1.5。因此,L-II內壓痕頂角的裂紋為巴氏裂紋。橫截面方向,L-III內的c/a>2.5或l/a>1.5,因此L-III內的裂紋為中位裂紋。
表1 壓痕法計算斷裂韌性的公式
壓痕法計算斷裂韌性KC的公式如表1所示(表1中,E為彈性模量,P為測試載荷,H為硬度),其相應的計算結果如表2所示。計算結果表明:在不考慮裂紋屬性的情況下,通過8種公式計算出的L-II的KC均高于L-III。且隨著測試載荷的提高,L-III內相應的KC顯著下降。造成這種現象的主要原因是隨著載荷的增加,邊緣效應的影響也顯著增加。
表2 表面強化層不同層內斷裂韌性的經驗計算值
結合裂紋類型的判斷結果,L-II內壓痕尖端的裂紋為巴氏裂紋,其可選用的公式為(7)和(8)。數據表明,L-II內的計算結果所表現出的趨勢與L-III的趨勢相反。提高測試載荷時,KC反而升高。在“硬殼-軟底”的基體效應造成明顯影響之前,壓痕尖端裂紋長度的延長并未與載荷的提高呈線性關系。結果表明,L-II內微米級組織表現出更優異的裂紋抗擴展能力,最終在壓痕裂紋上表現為短裂紋的現象。總之,從計算結果上來看,公式(7)的計算值與公式(8)有一定差異。由于公式(8)的提出是基于WC-Co合金,其具有相對較高的韌性,不一定適用于高硬、脆性材料。通過分析,公式(7)的計算結果隨載荷的變化差異較小,具有較高的可信度。前述壓痕形貌分析證明,當測試載荷為2N時,所得硬度為L-II的最可信硬度。選取2N載荷下裂紋長度和公式(7)的計算結果評價L-II的斷裂韌性,L-II的KC為4.58MPa·m1/2。
L-III內的裂紋為中位裂紋體系,適用公式為(1)~(6)。對于表2所示結果,公式(5)的計算結果偏差較大。因為公式(5)的適用條件為l/a≥1.5,而在載荷為0.5N時,壓痕的l/a<1.5。前述討論結果證明1N載荷下的硬度為L-III的最可信硬度。選取載荷為1N時壓痕的裂紋長度,計算L-III的斷裂韌性。因此,將1N載荷下的硬度和裂紋數據代入經驗公式(1)~(4)和(6),經計算,其KC均值為2.94MPa·m1/2,該計算結果可為L-III的斷裂韌性。相關研究的TiC、NbC涂層的斷裂韌性為3.1MPa·m1/2,NbC的斷裂韌性約為3.0MPa·m1/2。因此,高百分比、高致密的層狀(TiNb)C表面強化層具有高硬度,同時具有較好的韌性。
3、 結論
(TiNb)C表面強化層內,層狀結構導致其具有不同的顯微硬度和斷裂韌性,L-II具有更高的顯微硬度。受基底效應的影響,在2N的載荷下,L-II的顯微硬度為可信硬度,平均硬度為2594.13HV,可信斷裂韌性為4.58MPa·m1/2;受邊緣效應的影響,在1N的載荷下,L-III所得顯微硬度為可信硬度,平均硬度為2334.88HV,可信斷裂韌性為2.94MPa·m1/2。