來源：小小搬磚狗微信公眾號，作者：羅敏強。

首先介紹兩個名詞的概念。強度，是指物體抵抗破壞的能力，常用的強度性能指標為拉伸強度與屈服強度；剛度，是指物體抵抗變形的能力，用彈性模量E 來衡量。

任何固體在受到力的作用時，都會發生變形，這是材料力學研究的第一個大前提，針對變形的固體，又有以下四個假設來保證理論的成立。

• 連續性假設：即認為整個物體體積內毫無空隙地充滿物質。這是為了保證固體沒有內部缺陷，從而在分析計算時，不需要另外考慮由于固體內部的缺陷而導致的受力不均等問題。

   

• 均勻性假設：即認為物體內的任何部分，其力學性能相同。這是為了保證物體在受力時，各個部位傳遞力及強度、剛度相同，從而保證分析的連線性。

   

• 各向同性假設：認為在物體內各個不同方向的力學性能相同。這樣的規定保證了材料的線性，從而便于分析。

   

• 小變形假設：認為構件的變形極其微小，比構件本身尺寸要小得多。保證幾何學的線性，不需要進行復雜的幾何變換，降低了分析計算難度。

對于車輛的疲勞分析來說，最主要的還是桿件（車身部品是板件，但多考察其焊點處及部品安裝部的疲勞，因此，可類似于桿件的受力情況來進行分析），而桿件的受力形式主要是下圖中所示的拉伸壓縮、彎曲、扭轉、剪切這幾種。

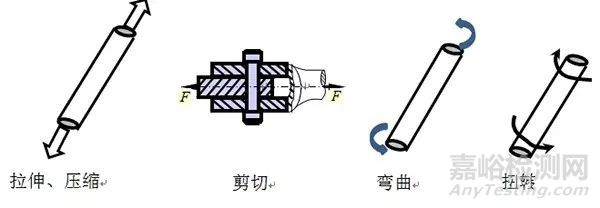
圖1 桿件載荷形式

由于拉伸與壓縮時的受力情況類似，下面僅以拉伸一種情況來討論這兩種受力。

圖2 桿受拉力圖

如上圖所示為一個受拉伸力的桿件，其受大小為F 的力拉伸后，軸向長度由l 變為l0，直徑由d 變成d0，至此引入線應變（正應變）的概念，線應變（軸向）為物體受力后的伸長量與原長度的比值，即

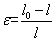
同時，徑向的應變為

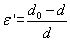
引入泊松比μ，泊松比定義為徑向正應變與軸向正應變的絕對值的比值，也叫橫向變形系數，它是反映材料橫向變形的彈性常數。表達式為：

汽車上常用幾種材料的泊松比參考值為：碳鋼 (0.24~0.29)，鑄鋼 (0.3)，合金鋼 (0.25~0.3)，軋制鋼 (0.31~0.34)，橡膠 (0.47)。

講到拉伸壓縮，還要介紹一個大家都很熟悉的定律：胡克定律，也就是經常說的彈性定律。其用方程式表達如下：

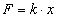
即在彈性范圍內，物體在力作用下所發生的變形與力的大小成正比。

物體在受到拉伸力后，其內部受到的力即為應力，應力定義為單位面積上所承受的附加內力。應力有正應力和切應力之分，正應力為與受力平面垂直的應力，切應力為沿著受力平面切線方向的力。例如，回到圖2，如果分析 ab 平面，則在整個平面內只有正應力，根據材料力學分析的連續性假設，則可知在整個 ab 平面上各點的應力大小是相同的，可知正應力的表達式為

式中，A 為 ab 平面的面積，但如果分析與 ab 平面呈β 角的 cd 面，根據正應力與切應力的定義，可知此時的正應力與切應力的表達式分別為

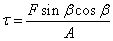
正應力與應變之間的比例系數定義為彈性模量（也叫楊氏模量）E，則有

既然正應力與應變之間有彈性模量的系數，那么剪切應力與剪切應變有沒有相應的系數呢，是有的！在討論正應力時提到了線應變，而用于描述剪切應力的應變為角應變，為什么要這樣做呢，原因可以從剪切應力對物體的破壞形式來分析，如下圖所示為圖1中物體受剪切力時的受力分析。

由受力分析可知，當物體受到剪切力時，力的破壞形式是使物體發生錯位變形，反映到某一平面上，即為平面發生了角度偏移，圖中的γ 定義為剪切應變，即在力作用下單位面積內角度的變化量。同樣剪切應變與切應力之間也存在比例關系，比例系數稱為剪切模量G，也叫切變模量，其表達式為

剪切模量與彈性模量之間存在如下關系

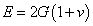
以上的分析是基于物體在拉伸及壓縮過程中變形較小，因而在計算應力過程中，始終認為受力面的面積及桿件長度不變，這種情況下計算出來的應力及應變稱為名義應力及名義應變。而我們知道，在桿件變形過程中，受力面的面積及桿件的長度也是隨之發生變化的，當變形較小時，近似認為變形前后面積及長度相等，誤差較小，可以接受；但當變形較大時，試件的幾何尺寸會發生明顯改變，此時再近似進行計算，將導致較大誤差。因此，對于大變形的情況，需要采用真應力及真應變來準確描述材料的特性。

真應力及真應變的計算方法，即用當前實時的橫截面面積及桿件長度l0 來進行計算的，則真應力計算公式為

真實應變的計算公式為

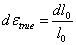
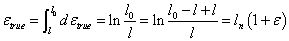
材料在拉伸過程中的力學性能用應力與應變的關系曲線來描述，也就是經典的四階段曲線，如下圖所示。

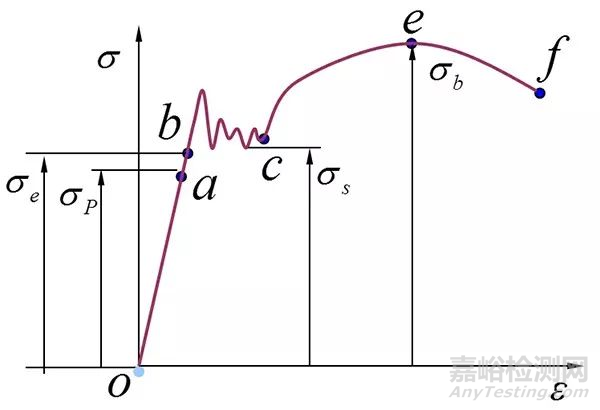
• 彈性階段（ob 段）：a 點處應力為比例極限，b 點處應力為彈性極限，這個階段的應力與應變呈線性關系，符合胡克定律。

   

• 屈服階段（bc 段）：c 點處應力為屈服極限，這個階段，材料逐漸失去抵抗變形的能力，在屈服點之后，應力與應變曲線通常稍微下降一點。

   

• 強化階段（ce 段）：e 點處應力為強度極限，這個階段，抵抗變形的能力恢復，這是由于應變硬化作用，應變繼續增加，直到極限拉伸應力。在到達極限拉伸應力之前，由于泊松比的限制，試件的橫截面積均勻縮小，在材料發生哪兒不匹配后，任何時刻卸去所施加的外力，應力會沿線性路徑下降到零，當應力回到零時，剩余的應變就是塑性應變。如果試件重新施加外力，材料會出現彈性變形，直到達到前一次卸載時的應力水平，而后應力應變關系將隨著外力的進一步施加而再一次變成非線性關系。這也就相當于在重新加載過程中，材料的比例極限上升了，這種現象稱為冷作硬化。

   

• 局部頸縮階段（ef 段）：在達到強度極限后繼續施加載荷，試件的變形將變得不穩定，變形開始集中于一個很窄的區域，隨著力的繼續施加，當縮頸達到一定極限后，試件將發生斷裂。

當材料發生斷裂后，斷后伸長率定義為試件斷后長度的增長量與原長的比值，大于5%的稱為塑性材料，低于5%的稱為脆性材料。對于某些韌性較差的塑性材料或脆性材料，往往沒有明顯的屈服階段，因此也就沒有明確的屈服點。對于這些材料，通常用0.2%殘余變形的應力值為其屈服極限，稱為條件屈服極限。具體做法為，在應力應變橫坐標應變為0.2%的地方，畫一條斜線，斜率為彈性模量，斜線與曲線的交點即為屈服點，這個數據經常用于鋁制品、中高碳鋼，有時候也適用于低碳鋼。

受到彎曲作用的桿件稱作為梁，存在以下幾種靜定梁形式。

在分析純彎曲的正應力時，基于以下假設：橫截面變形后保持為平面，且仍然垂直于變形后的梁軸線，只是繞截面內某一軸線偏轉了一個角度。梁可以看作是無數層縱向纖維平面組成，當梁受到彎曲扭矩時，纖維長度不變的平面稱為中性面，中性面橫截面的交線稱為中性軸。

下面介紹彎曲正應力的求法。建立如圖所示的坐標軸，圖中oo 與o‘o’ 為中性面，則其再變形前后的長度均為dx=ρdθ，而變形后bb 的長度、b'b' 的長度變為 (ρ+y)dθ，可知應變為ε=y/ρ，應力為σ=Ey/ρ，式中y 值是容易得到的，但曲率半徑ρ 是不能直接得到的，因此有必要將其轉換為容易得到的參數。

觀察受彎矩的平面，由靜力學平衡可知，在整個平面內正應力產生的抵抗彎矩與所受到的彎矩相等，建立方程為

則得到

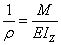
式中，IZ=∫Ay²dA 稱為截面系數，則正應力方面變成

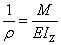
由上式可知：正應力大小與其到中性軸距離成正比，中性軸上，正應力等于零。幾種常見形狀的截面系數如下圖所示

• 梁的跨度較短（長高比小于5）；

   

• 在支座附近作用較大載荷（載荷靠近支點）；

   

• 鉚接或焊接的工字形或箱形等截面梁（腹板、焊縫、膠合面或鉚釘等）；

   

• 彎曲切應力的求法可參照本文參考文獻中的內容進行學習。

細化成下圖所示的詳細變形情況，在變形微小的情況下，有如下假設成立：圓弧的長度與該圓弧兩點間的距離相等，撓角小時，在微小單元中，沿y 軸方向的變形與沿x 軸方向變形的比例等于撓角。

則由圖可建立以下方程式

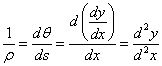
又，M=EIZ/ρ，得到撓曲線微分方程為

實際應用過程中，配合固定點處的初始條件，即可得到撓曲線的表達式。

扭轉的受力及變形特點是，桿件受到大小相等，方向相反且作用平面垂直于桿件軸線的力偶作用，桿件的橫截面繞軸線產生相對轉動。

受扭轉力矩作用的一般為旋轉部件，軸所受的扭矩與輸入功率及轉速的關系為

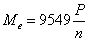
由此可看出，在功率相同情況下，隨著轉速升高，扭矩是減小的。

下面來計算扭轉應力，下圖為軸受扭矩時的變形圖。

由圖可知有下式成立

得出距圓心處的切應變為：

則切應力為：

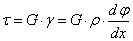
又根據下圖所示建立靜力學關系

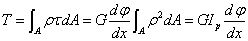
得到

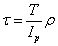
即切應力在徑向的分布是與半徑成正比的，在圓心處為零，這樣也解釋了為什么有些僅受扭矩的零件是空心的，因為在靠近圓心處，零件所承受的切應力很小，即使將這部分切去，也對軸的抗扭變形能力影響不大，但是卻能節省材料。

參考文獻：

劉鴻文. 材料力學第5版[M]. 高等教育出版社.2011.

蘇旭明，鄭鑫，李大永.汽車設計的耐久性分析[M].機械工業出版社.2016